题目内容
3. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.(1)求抛物线的解析式并直接写出点D的坐标;
(2)求△BCD的面积;
(3)点P为直线x=1右方抛物线上的一点(点P不与点B重合),记A、B、C、P四点所构成的四边形面积为S,若S=$\frac{5}{2}$S△BCD,求点P的坐标.
分析 (1)利用抛物线的对称性确定B(3,0),则设交点式y=a(x+1)(x-3),然后将C(0,-3)代入求出a即可得到抛物线的解析式,再把解析式配成顶点式即可得D的坐标;
(2)先利用待定系数法求出直线BC的解析式为y=x-3,则求出E(1,-2),然后根据三角形面积公式,利用S△BCD=S△CDE+S△BDE进行计算即可;
(3)设P点坐标为(t,t2-2t-3),讨论:当点P在x轴下方时,即1<m<3时,连结OP,如图1,根据三角形面积公式,利用S=S△AOC+S△POC+S△POB得到S=-$\frac{3}{2}$t2+$\frac{9}{2}$t+6,则利用S=$\frac{5}{2}$S△BCD得到2-$\frac{3}{2}$t2+$\frac{9}{2}$t+6=$\frac{5}{2}$×3,解方程得t1=$\frac{3+\sqrt{5}}{2}$,t2=$\frac{3-\sqrt{5}}{2}$(舍去),于是得到此时P点的坐标为($\frac{3+\sqrt{5}}{2}$,$\frac{-3+\sqrt{5}}{2}$);当点P在轴的上方时,即m>3,如图2,同样方法得到2t2-4t=$\frac{5}{2}$×3,解方程得t1=$\frac{2+\sqrt{19}}{2}$,t2=$\frac{2-\sqrt{19}}{2}$(舍去),所以此时P点的坐标为($\frac{2+\sqrt{19}}{2}$,$\frac{3}{4}$).
解答 解:(1)∵点A(-1,0)和点B关于直线x=1对称,
∴B(3,0),
设抛物线解析式为y=a(x+1)(x-3),
将C(0,-3)代入得-3=-3a,解得a=1,
∴抛物线的解析式为y=x2-2x-3,
∵y=(x-1)2+4,
∴抛物线的顶点D的坐标为(1,-4);
(2)设直线BC的解析式为y=mx+n,
把C(0,-3),B(3,0)代入得$\left\{\begin{array}{l}{n=-3}\\{3m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{n=-3}\end{array}\right.$,
∴直线BC的解析式为y=x-3,
当x=1时,y=x-3=-2,则E(1,-2),
∴S△BCD=S△CDE+S△BDE=$\frac{1}{2}$×(4-2)×1+$\frac{1}{2}$×(4-2)×2=3;
(3)设P点坐标为(t,t2-2t-3),
当点P在x轴下方时,即1<m<3时,连结OP,如图1,
∵S=S△AOC+S△POC+S△POB=$\frac{1}{2}$×1×3+$\frac{1}{2}$×3×t+$\frac{1}{2}$×3(-t2+2t+3)=-$\frac{3}{2}$t2+$\frac{9}{2}$t+6,
而S=$\frac{5}{2}$S△BCD,
∴-$\frac{3}{2}$t2+$\frac{9}{2}$t+6=$\frac{5}{2}$×3,
整理得t2-3t+1=0,解得t1=$\frac{3+\sqrt{5}}{2}$,t2=$\frac{3-\sqrt{5}}{2}$(舍去),此时P点的坐标为($\frac{3+\sqrt{5}}{2}$,$\frac{-3+\sqrt{5}}{2}$);
当点P在轴的上方时,即m>3,如图2,
∵S=S△ABC+S△PAB=$\frac{1}{2}$×4×3+$\frac{1}{2}$×4(t2-2t-3)=2t2-4t,
而S=$\frac{5}{2}$S△BCD
∴2t2-4t=$\frac{5}{2}$×3,
整理得4t2-8t-15=0,解得t1=$\frac{2+\sqrt{19}}{2}$,t2=$\frac{2-\sqrt{19}}{2}$(舍去),此时P点的坐标为($\frac{2+\sqrt{19}}{2}$,$\frac{3}{4}$),
综上所述,满足条件的P点坐标为($\frac{3+\sqrt{5}}{2}$,$\frac{-3+\sqrt{5}}{2}$)或($\frac{2+\sqrt{19}}{2}$,$\frac{3}{4}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;理解坐标与图形的性质,记住三角形的面积公式;会解一元二次方程;会运用分类讨论的思想解决数学问题.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | ±8 | C. | 8或2 | D. | ±8或±2 |
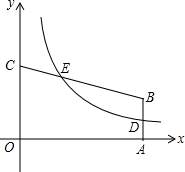 如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )
如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )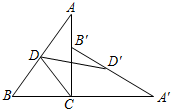 如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长.
如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长. 如图所示,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=45°.
如图所示,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=45°.