题目内容
15.一次会议上,每两个参加会议的人都相互握一次手,一共握手45次,则参加会议的人数是10.分析 设参加会议有x人,每个人都与其他(x-1)人握手,共握手次数为 $\frac{1}{2}$x(x-1),根据题意列方程即可.
解答 解:设参加会议有x人,
依题意得:$\frac{1}{2}$x(x-1)=45,
整理得:x2-x-90=0
解得x1=10,x2=-9,(舍去).
答:参加这次会议的有10人,
故答案为:10.
点评 本题主要考查了一元二次方程的应用,计算握手次数时,每两个人之间产生一次握手现象,故共握手次数为$\frac{1}{2}$x(x-1),此题难度不大.

练习册系列答案
相关题目
5.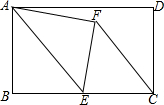 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.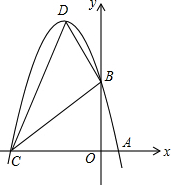 已知:m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(m,0),B(0,n).
已知:m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(m,0),B(0,n).