题目内容
1.第四象限内的点P到x轴的距离是3,到y轴的距离是5,则点P的坐标是(5,-3).分析 根据点到x轴的距离是纵坐标的绝对值,点到y轴的距离是横坐标的绝对值,第四象限内点的横坐标大于零,纵坐标小于零,可得答案.
解答 解:由点P到x轴的距离是3,到y轴的距离是5,得
|y|=3,|x|=5.
由第四象限内点的横坐标大于零,纵坐标小于零,得
点P的坐标是(5,-3),
故答案为:(5,-3).
点评 本题考查了点的坐标,点到x轴的距离是纵坐标的绝对值,点到y轴的距离是横坐标的绝对值,第四象限内点的横坐标大于零,纵坐标小于零.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.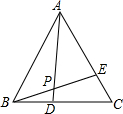 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
9.下列各式中①$\sqrt{\frac{1}{2}}$,②$\sqrt{2x}$,③$\sqrt{{x}^{3}}$,④$\sqrt{-5}$,⑤$\root{3}{5}$,二次根式的个数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列计算正确的是( )
| A. | ($\sqrt{2}$)2=2 | B. | $\sqrt{3}$-$\sqrt{2}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=3 | D. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ |
13.已知二元一次方程有一个解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,那么这个二元一次方程可能是( )
| A. | x+y=3 | B. | x-y=1 | C. | 2x+y=3 | D. | 2x-y=1 |
10.函数y=$\sqrt{x-6}$的自变量x的取值范围是( )
| A. | x>6 | B. | x<6 | C. | x≥6 | D. | x≤6 |
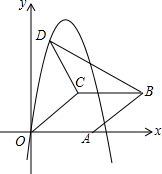 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.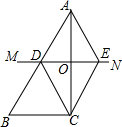 如图,在△ABC中,边AC的垂直平分线MN与AB边交于点D,与AC边交于点O,CE∥AB与MN交于点E,连接AE、CD,求证:四边形ADCE是菱形.
如图,在△ABC中,边AC的垂直平分线MN与AB边交于点D,与AC边交于点O,CE∥AB与MN交于点E,连接AE、CD,求证:四边形ADCE是菱形.