题目内容
16.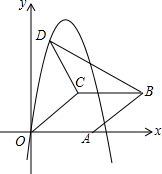 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.
分析 设D(x,-x2+6x),根据勾股定理求得OC,根据菱形的性质得出BC,然后根据三角形面积公式得出∴S△BCD=$\frac{1}{2}$×5×(-x2+6x-3)=-$\frac{5}{2}$(x-3)2+15,根据二次函数的性质即可求得最大值.
解答 解:∵D是抛物线y=-x2+6x上一点,
∴设D(x,-x2+6x),
∵顶点C的坐标为(4,3),
∴OC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵四边形OABC是菱形,
∴BC=OC=5,BC∥x轴,
∴S△BCD=$\frac{1}{2}$×5×(-x2+6x-3)=-$\frac{5}{2}$(x-3)2+15,
∵-$\frac{5}{2}$<0,
∴S△BCD有最大值,最大值为15,
故答案为15.
点评 本题考查了菱形的性质,二次函数的性质,注意数与形的结合是解决本题的关键.

练习册系列答案
相关题目
6.点P(-2,-3)向右平移2个单位,再向下平移3个单位,则所得到的点的坐标为( )
| A. | (0,0) | B. | (-4,0) | C. | (0,-6) | D. | (0,6) |
6.学校为同学们进行体检,某班学生右眼视力检测结果如表:
该班学生视力的众数、中位数分别是( )
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 5 | 4 | 3 | 5 | 1 | 2 | 5 | 9 | 6 |
| A. | 5,4 | B. | 4.5,4.5 | C. | 4.9,4.7 | D. | 4.9,4.5 |
 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示: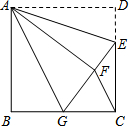 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论: