题目内容
11.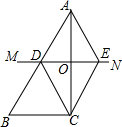 如图,在△ABC中,边AC的垂直平分线MN与AB边交于点D,与AC边交于点O,CE∥AB与MN交于点E,连接AE、CD,求证:四边形ADCE是菱形.
如图,在△ABC中,边AC的垂直平分线MN与AB边交于点D,与AC边交于点O,CE∥AB与MN交于点E,连接AE、CD,求证:四边形ADCE是菱形.
分析 根据中垂线的性质中垂线上的点线段两个端点的距离相等可得出AE=CE,AD=CD,OA=OC∠AOD=∠EOC=90°,再结合CE∥AB,可证得△ADO≌△CEO,从而根据由一组对边平行且相等知,四边形ADCE是平行四边形,结合OD=OE,OA=OC,∠AOD=90°可证得为菱形.
解答 证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,∠AOD=∠EOC=90°,
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO.(ASA)
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,
∴四边形ADCE是平行四边形
又∵∠AOD=90°,
∴?ADCE是菱形.
点评 本题考查了菱形的判定及线段垂直平分线的性质,利用了:中垂线的性质;全等三角形的判定和性质;平行四边形和菱形的判定.

练习册系列答案
相关题目
19.已知:?ABCD周长为30cm,相邻两边之比为3:2,则它的两邻边长度分别为( )
| A. | 18cm,12cm | B. | 6cm,4cm | C. | 9cm,6cm | D. | 12cm,8cm |
6.学校为同学们进行体检,某班学生右眼视力检测结果如表:
该班学生视力的众数、中位数分别是( )
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 5 | 4 | 3 | 5 | 1 | 2 | 5 | 9 | 6 |
| A. | 5,4 | B. | 4.5,4.5 | C. | 4.9,4.7 | D. | 4.9,4.5 |
16.?ABCD中,周长等于24,其中一组对边长是8,那么,另一组对边长为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
3.下列平面图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
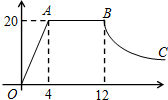 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.如图是某天大棚内温度y(℃)随时间x(小时)变化的函数图象,其中OA段是系统开启后的升温阶段,y与x成正比例,BC段是系统关闭后的降温阶段,y与x成反比例.请根据图中信息解答下列问题:
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.如图是某天大棚内温度y(℃)随时间x(小时)变化的函数图象,其中OA段是系统开启后的升温阶段,y与x成正比例,BC段是系统关闭后的降温阶段,y与x成反比例.请根据图中信息解答下列问题: