题目内容
14．
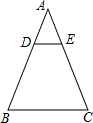如图，若DE∥BC，则下列式子不成立的是（ ）| A． | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B． | $\frac{AD}{AB}$=$\frac{EC}{AC}$ | C． | $\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$ | D． | $\frac{BD}{AB}$=$\frac{EC}{AC}$ |
分析 根据平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例解答即可．
解答 解：∵DE∥BC，
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$，A成立；
$\frac{AD}{AB}$=$\frac{AE}{AC}$，B不成立；
$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$，C成立；
$\frac{BD}{AB}$=$\frac{EC}{AC}$，D成立，
故选：B．
点评 本题考查平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
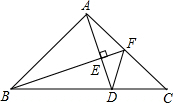△ABC中，∠BAC=90°，AB=AC，F为AC中点，连接BF作AE⊥BF交BF于E，交BC于D，求证：∠AFB=∠CFD．