题目内容
19.有一幅长20cm、宽16cm的照片,现要为这幅照片配一个四条边宽度相同的相框,且相框边所占面积为照片面积的二分之一,求相框边的宽度.分析 设镜框边宽度为x,则镜框长为(20+2x),宽为(16+2x),完整图形面积为照片面积的(1+$\frac{1}{2}$),依题意列方程求解.
解答 解:设相框边的宽度为x cm,则可列方程:
(20+2x)(16+2x)=(1+$\frac{1}{2}$)×20×16,
解得:x1=2,x2=-20(舍去),
答:相框边的宽度为2cm.
点评 此题考查一元二次方程的实际运用,设未知数来表示整个图形的长、宽,再利用整个图形面积与相片面积的关系列方程解决问题.

练习册系列答案
相关题目
14.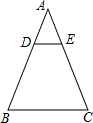 如图,若DE∥BC,则下列式子不成立的是( )
如图,若DE∥BC,则下列式子不成立的是( )
 如图,若DE∥BC,则下列式子不成立的是( )
如图,若DE∥BC,则下列式子不成立的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{EC}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$ | D. | $\frac{BD}{AB}$=$\frac{EC}{AC}$ |
 将图中平面展开图折叠成正方体后,相对面上的两个数互为相反数,则x+y+z=-1.5.
将图中平面展开图折叠成正方体后,相对面上的两个数互为相反数,则x+y+z=-1.5. 如图,OA反向延长得射线OE,线段CD向两方延长得直线CD.
如图,OA反向延长得射线OE,线段CD向两方延长得直线CD.