题目内容
2.观察下列各式:1=12,1+3=22,1+3+5=32,1+3+5+7=42,…
根据前面各式的规律,可猜测:1+3+5+7+9+…+(2n+1)=(n+1)2(n为自然数).
分析 由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出连续奇数的和等于数的个数的平方;第n+1个奇数表示为2(n+1)-1,因此得到一般规律解决问题.
解答 解:∵1=12,
1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
…
∴1+3+5+7+…+(2n+1)=(n+1)2.
故答案为:(n+1)2.
点评 此题考查数字的变化规律,找出从奇数1开始,连续奇数的和等于数的个数的平方是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
17.下列四个选项中,变形正确的是( )
| A. | a+(b+c)=ab+c | B. | a2-[-(-a+b)]-a2-a+b=a2-a+b | ||
| C. | a+2(b-c)=a+2b-c | D. | a-(b+c-d)=a-b-c+d |
14.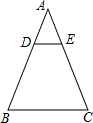 如图,若DE∥BC,则下列式子不成立的是( )
如图,若DE∥BC,则下列式子不成立的是( )
 如图,若DE∥BC,则下列式子不成立的是( )
如图,若DE∥BC,则下列式子不成立的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{EC}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$ | D. | $\frac{BD}{AB}$=$\frac{EC}{AC}$ |
12. 如图,直线AB与CD相交于点O,OB平分∠DOE.若∠BOE=35°,则∠COE的度数是( )
如图,直线AB与CD相交于点O,OB平分∠DOE.若∠BOE=35°,则∠COE的度数是( )
 如图,直线AB与CD相交于点O,OB平分∠DOE.若∠BOE=35°,则∠COE的度数是( )
如图,直线AB与CD相交于点O,OB平分∠DOE.若∠BOE=35°,则∠COE的度数是( )| A. | 35° | B. | 70° | C. | 105° | D. | 110° |
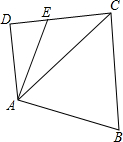 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$