题目内容
19.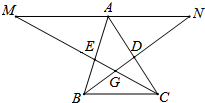 如图,△ABC中,AB=7,BC=6,AC=8,延长∠ABC、∠ACB的角平分线BD、CE分别交过点A且平行于BC的直线于N、M,BD与CE相交于点G,则△BCG与△MNG的面积之比是4:25.
如图,△ABC中,AB=7,BC=6,AC=8,延长∠ABC、∠ACB的角平分线BD、CE分别交过点A且平行于BC的直线于N、M,BD与CE相交于点G,则△BCG与△MNG的面积之比是4:25.
分析 根据角平分线的性质求出$\frac{BC}{MN}$=$\frac{2}{5}$,根据相似三角形的面积比等于相似比的平方解答.
解答 解:∵CE是∠ACB的角平分线,
∴$\frac{AE}{EB}$=$\frac{AC}{BC}$=$\frac{8}{6}$=$\frac{4}{3}$,
∵MN∥BC,
∴$\frac{AM}{BC}$=$\frac{AE}{EB}$=$\frac{4}{3}$,
同理,$\frac{AN}{BC}$=$\frac{AD}{DC}$=$\frac{AB}{BC}$=$\frac{7}{6}$,
∴$\frac{BC}{MN}$=$\frac{2}{5}$,
∵MN∥BC,
∴△BCG∽△MNG,
∴△BCG与△MNG的面积之比是4:25.
故答案为:4:25.
点评 本题考查的是角平分线性质定理和相似三角形的判定定理、性质定理,掌握三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例是解题的关键.

练习册系列答案
相关题目
9.抛物线y=-2x2-3与双曲线y=-$\frac{1}{x}$的交点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.如果关于x的一元二次方程x2-4x+k=0有两个相等的实数根,那么k的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |