题目内容
6.(1)计算:$\sqrt{9}$+($\frac{1}{2017}$)0+|-1|.(2)计算:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{9}^{2}}$)(1-$\frac{1}{1{0}^{2}}$).
分析 (1)原式利用算术平方根定义,零指数幂法则,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方差公式变形,计算即可得到结果.
解答 解:(1)原式=3+1+1=5;
(2)原式=(1+$\frac{1}{2}$)(1-$\frac{1}{2}$)(1+$\frac{1}{3}$)(1-$\frac{1}{3}$)…(1+$\frac{1}{9}$)(1-$\frac{1}{9}$)(1+$\frac{1}{10}$)(1-$\frac{1}{10}$)=$\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{9}{10}$×$\frac{3}{2}$×$\frac{4}{3}$×…×$\frac{11}{10}$=$\frac{1}{10}$×$\frac{11}{2}$=$\frac{11}{20}$.
点评 此题考查了平方差公式,以及实数的运算,熟练掌握公式及运算法则是解本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
17.已知从n个人中,选出m个人按照一定的顺序排成一行,所有不同的站位方法有n×(n-1)×…×(n-m+1)种.现某校九年级甲、乙、丙、丁4名同学和1位老师共5人在毕业前合影留念(站成一行).若老师站在中间,则不同的站位方法有( )
| A. | 6种 | B. | 20种 | C. | 24种 | D. | 120种 |
15. 如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
 如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )| A. | 36° | B. | 46° | C. | 27° | D. | 63° |
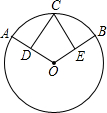 如图,在⊙O中,$\widehat{AC}$=$\widehat{CB}$,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.
如图,在⊙O中,$\widehat{AC}$=$\widehat{CB}$,CD⊥OA于D,CE⊥OB于E,求证:AD=BE. 如图,正方形ABCD内接于⊙O,如果圆的半径为6,那么这个正方形的边长为6$\sqrt{2}$.
如图,正方形ABCD内接于⊙O,如果圆的半径为6,那么这个正方形的边长为6$\sqrt{2}$. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.