��Ŀ����
12����ij�ּ���ͼ�θ������¶��壺����һ�������Ķ������γɵ�ͼ�Σ�����������������ĵ�Ĺ켣�����磬ƽ���ڵ�����ľ�����ڶ����ĵ�Ĺ켣�����Զ���ΪԲ�ģ�����Ϊ�뾶��Բ����1����ͼ1���ڡ�ABC�У�AB=AC����BAC=90�㣬A��0��2����B��x����һ���㣬����B��x�����˶�ʱ����C������ϵ���˶�����C�˶��γɵĹ켣��ֱ��DE����DE��x���ڵ�G����ֱ��DE�ı���ʽ��x=2��
��2������ABC�ǵȱ�������ʱ���ڣ�1���������£�����C�γɵĹ켣Ҳ��һ��ֱ�ߣ�
�ٵ���B�˶�����ͼ2��λ��ʱ��AC��x�ᣬ��C��������ǣ�$\frac{4\sqrt{3}}{3}$��2����
���ڱ���ͼ�л�������C�γ�ֱ�ߵ�ʾ��ͼ�����������ֱ�ߵı���ʽ��
�����������ֱ�߷ֱ���x��y�ύ��E��F���㣬����C���߶�EF���˶�ʱ����H���߶�OF���˶���������O��F�غϣ�����CH=CE����CE��ȡֵ��Χ��$\frac{4\sqrt{3}}{9}$��CE��$\frac{2\sqrt{3}}{3}$��
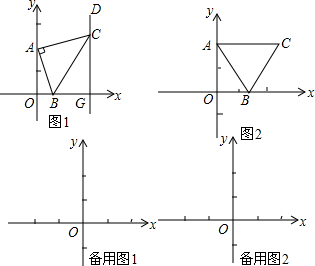
���� ��1����C��CM��y�ᣬ��DMA�ա�AOB�������DM�ij����ɵó�DE�ı���ʽ��
��2���ٹ�C��CN��x���ڵ�N���ɵȱ������ε����ʿ����CN��ON�������C�����ꣻ�ڿ����������������һ��C�㣬�統C��0��-2��ʱ���������������ô���ϵ�����������ֱ�߱���ʽ������CΪԲ�ģ�CE��Ϊ�뾶��Բ������Բ����Oʱ����ʱCE�����ֵ��ȡ������ֵ��������Բ��y������ʱ��CE����Сֵ���ٸ��ݵ��������κ�ƽ���߷��߶γɱ����ֱ����CE��ֵ��������ô𰸣�
��� �⣺
��1����C��CM��y���ڵ�M����ͼ1��
�ߡ�BAC=90�㣬
���CAM+��BAO=��MCA+��CAM=90�㣬
���BAO=��MCA��
�ڡ�DMA�͡�AOB��
$\left\{\begin{array}{l}{��MCA=��BAO}\\{��CMA=��AOB}\\{AC=AB}\end{array}\right.$
���DMA�ա�AOB��AAS����
��MC=OA=2����DE��x�ᣬ
��ֱ��DE�ı���ʽΪx=2��
�ʴ�Ϊ��x=2��
��2���ٹ�C��CN��x���ڵ�N����ͼ2��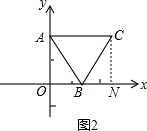
��AC��x�ᣬ
��CN=AO=2��
�֡�ABCΪ�ȱ������Σ�
���ACB=60�㣬
���BCN=30�㣬
��AC=BC=$\frac{CN}{cos30��}$=$\frac{4\sqrt{3}}{3}$��
��C��������$\frac{4\sqrt{3}}{3}$��2����
�ʴ�Ϊ����$\frac{4\sqrt{3}}{3}$��2����
���ɢ�֪C������Ϊ��$\frac{4\sqrt{3}}{3}$��2����
�ҵ�C��0��-2��ʱ����A��C����x��Գƿ�֪��x���ϴ���B��ʹ��ABCΪ�ȱ������Σ�
��㣨0��-2��Ҳ��C�����γɵ�ֱ���ϣ�
��ֱ�߱���ʽΪy=kx+b��
�ѵ㣨$\frac{4\sqrt{3}}{3}$��2���ͣ�0��-2������ɵ�$\left\{\begin{array}{l}{-2=b}\\{2=\frac{4\sqrt{3}}{3}k+b}\end{array}\right.$�����$\left\{\begin{array}{l}b=-2\\ k=\sqrt{3}\end{array}\right.$��
��ֱ�ߵı���ʽ��y=$\sqrt{3}$x-2��
����C�˶��γ�ֱ����ͼ3��ʾ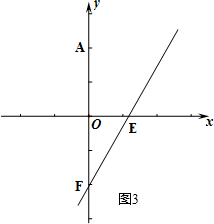
�۵���C���߶�EF��ʱ����CΪԲ�ģ�CE��Ϊ�뾶��Բ��
��Բ����Oʱ����ͼ4���߽�CO����֪��ʱCE���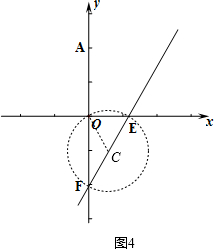
�ɢڿ����E������Ϊ��$\frac{2\sqrt{3}}{3}$��0����F��0��-2����
�ɹ��ɶ��������EF=$\frac{4\sqrt{3}}{3}$��
��Բ�ܽǶ�����֪��ʱCE=$\frac{1}{2}$EF=$\frac{2\sqrt{3}}{2}$��
��Բ��y������ʱ�����е㼴Ϊ���������ĵ�H������CH����ͼ5��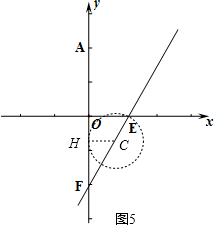
��ʱCE��ֵʱС��
��HC��OE����CH=CE��
��$\frac{HC}{OE}$=$\frac{FC}{EF}$=$\frac{EF-CE}{EF}$=$\frac{CE}{OE}$����$\frac{\frac{4\sqrt{3}}{3}-CE}{\frac{4\sqrt{3}}{3}}$=$\frac{CE}{\frac{2\sqrt{3}}{3}}$�����CE=$\frac{4\sqrt{3}}{9}$��
�ֵ�H��O��F���غϣ�
��CEȡ�������ֵ��
��CE��ȡֵ��ΧΪ$\frac{4\sqrt{3}}{9}$��CE��$\frac{2\sqrt{3}}{3}$��
�ʴ�Ϊ��$\frac{4\sqrt{3}}{9}$��CE��$\frac{2\sqrt{3}}{3}$��
���� ������Ҫ����һ�κ������ۺ�Ӧ�ã��漰֪ʶ����ȫ�������ε��ж������ʡ�����ϵ�������ȱ������ε����ʡ�Բ���й����ʵȣ��ڣ�1�������C��y��ľ����ǽ���Ĺؼ����ڣ�2������ȷ����CE�����ֵ����Сֵ�ǽ���Ĺؼ�������֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| �ɼ����Σ� | 43 | 45 | 46 | 47 | 48 | 49 | 51 |
| ���� | 2 | 3 | 5 | 7 | 4 | 2 | 2 |
| A�� | 47��46 | B�� | 47��47 | C�� | 45��48 | D�� | 51��47 |
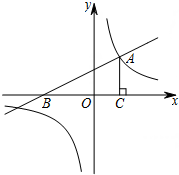 ��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��2��m����
��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��2��m����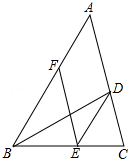 ��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ���E��F�ֱ���BC��AB�ϣ���DE��AB��BE=AF��
��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ���E��F�ֱ���BC��AB�ϣ���DE��AB��BE=AF��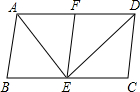 ��ͼ����֪ƽ���ı���ABCD������DE�۵����C����AD���ϵ�F����
��ͼ����֪ƽ���ı���ABCD������DE�۵����C����AD���ϵ�F����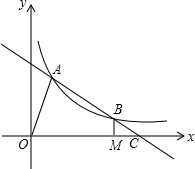 ��ͼ��ֱ��AB��˫����y=$\frac{k}{x}$��x��0����A��B���㣬��x���ڵ�C��4a��0����AB=2BC������B��BM��x���ڵ�M������OA����OM=3MC��S��OAC=8����k��ֵ��
��ͼ��ֱ��AB��˫����y=$\frac{k}{x}$��x��0����A��B���㣬��x���ڵ�C��4a��0����AB=2BC������B��BM��x���ڵ�M������OA����OM=3MC��S��OAC=8����k��ֵ��