题目内容
7.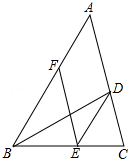 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
分析 (1)由BD是△ABC的角平分线,DE∥AB,易证得△BDE是等腰三角形,且BE=DE;又由BE=AF,可得DE=AF,即可证得四边形ADEF是平行四边形;
(2)首先过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,由∠ABC=60°,BD是∠ABC的平分线,可求得DG的产,继而求得DE的长,则可求得答案.
解答 (1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
(2)解:过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,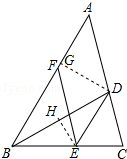
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠ABD=∠EBD=30°,
∴DG=$\frac{1}{2}$BD=$\frac{1}{2}$×4=2,
∵BE=DE,
∴BH=DH=2,
∴BE=$\frac{BH}{cos30°}$=$\frac{4}{3}\sqrt{3}$,
∴DE=$\frac{4}{3}\sqrt{3}$,
∴四边形ADEF的面积为:DE•DG=$\frac{8}{3}\sqrt{3}$.
点评 此题考查了平行四边形的判定与性质、等腰三角形的判定与性质以及三角函数等知识.注意掌握辅助线的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (x+y)(x-y) | C. | (x+y)(-x-y) | D. | (-x-y)(-x+y) |
15.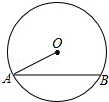 如图,已知⊙O的半径为10,弦AB长为16,则点O到AB的距离是( )
如图,已知⊙O的半径为10,弦AB长为16,则点O到AB的距离是( )
 如图,已知⊙O的半径为10,弦AB长为16,则点O到AB的距离是( )
如图,已知⊙O的半径为10,弦AB长为16,则点O到AB的距离是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
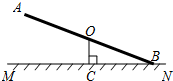 如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm.
如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm.