题目内容
2.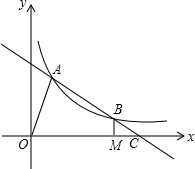 如图,直线AB交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C(4a,0),AB=2BC,过点B作BM⊥x轴于点M,连接OA,若OM=3MC,S△OAC=8,求k的值.
如图,直线AB交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C(4a,0),AB=2BC,过点B作BM⊥x轴于点M,连接OA,若OM=3MC,S△OAC=8,求k的值.
分析 连结OB,设B点坐标为(a,b),将B点坐标代入反比例解析式得到ab=k,确定出OM与BM的长,根据OM=3MC,表示出MC长,进而表示出三角形BOM与三角形BMC的面积,两面积之和表示出三角形BOC的面积,由AB=2BC,设点O到AC的距离为h,求出三角形BOC与三角形AOB面积之比,确定出三角形AOC的面积,由S△OAC=8列出关于k的方程,解方程即可求出k的值.
解答  解:连结OB,设B(a,b).
解:连结OB,设B(a,b).
∵点B在函数y=$\frac{k}{x}$上,
∴ab=k,且OM=a,BM=b,
∵OM=3MC,
∴MC=$\frac{1}{3}$a,
∴S△BOM=$\frac{1}{2}$ab=$\frac{1}{2}$k,S△BMC=$\frac{1}{2}$×$\frac{1}{3}$ab=$\frac{1}{6}$ab=$\frac{1}{6}$k,
∴S△BOC=S△BOM+S△BMC=$\frac{1}{2}$k+$\frac{1}{6}$k=$\frac{2}{3}$k,
∵AB=2BC,设点O到AC的距离为h,
则$\frac{{S}_{△BOC}}{{S}_{△AOB}}$=$\frac{\frac{1}{2}BC•h}{\frac{1}{2}AB•h}$=$\frac{BC}{AB}$=$\frac{1}{2}$,
∴S△AOB=2S△BOC=$\frac{4}{3}$k,
∴S△AOC=S△AOB+S△BOC=$\frac{4}{3}$k+$\frac{2}{3}$k=2k,
∵S△AOC=8,
∴2k=8,
∴k=4.
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
13.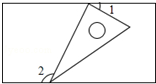 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )| A. | 155° | B. | 135° | C. | 125° | D. | 115° |
10.2015的倒数是( )
| A. | -2015 | B. | $-\frac{1}{2015}$ | C. | $\frac{1}{2015}$ | D. | 2015 |
7. 如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$平方厘米,则此方格纸的面积为( )
如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$平方厘米,则此方格纸的面积为( )
 如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$平方厘米,则此方格纸的面积为( )
如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$平方厘米,则此方格纸的面积为( )| A. | 11平方厘米 | B. | 12平方厘米 | C. | 13平方厘米 | D. | 14平方厘米 |
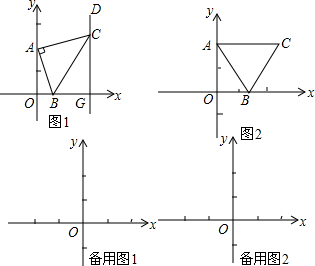
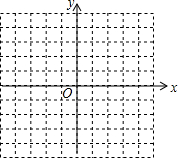 在同一平面直角坐标系中画出下列函数的图象,并指出它们的共同之处.
在同一平面直角坐标系中画出下列函数的图象,并指出它们的共同之处.