题目内容
19. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
分析 多边形的外角和为360°每一个外角都为24°,依此可求边数,多边形的周长即为所求.
解答 解:∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走了:15×10=150米.
故答案为:150.
点评 本题考查多边形的内角和计算公式,多边形的外角和.关键是根据多边形的外角和及每一个外角都为24°求边数.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )
| x | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 |
| ax2+bx+c | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 |
| A. | -$\frac{1}{2}$<x1<0,$\frac{3}{2}$<x2<2 | B. | -1<x1<-$\frac{1}{2}$,2<x2<$\frac{5}{2}$ | ||
| C. | -$\frac{1}{2}$<x1<0,2<x2<$\frac{5}{2}$ | D. | -1<x1<-$\frac{1}{2}$,$\frac{3}{2}$<x2<2 |
 如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.
如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.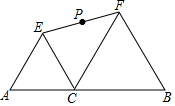 如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.
如图,线段AB=2,C是AB上一动点,以AC、BC为边在AB同侧作正△ACE、正△BCF,连EF,点P为EF的中点.当点C从A运动到B时,P点运动路径长为1.