题目内容
13．已知α是锐角，且cosα的值为$\frac{4}{5}$，则tanα=$\frac{3}{4}$．分析 根据同角三角函数关系：sin2α+cos2α=1，tanα=$\frac{sinα}{cosα}$，可得答案．
解答 解：由α是锐角，且cosα的值为$\frac{4}{5}$，得
sinα=$\sqrt{1-co{s}^{2}α}$=$\sqrt{1-（\frac{4}{5}）^{2}}$=$\frac{3}{5}$，
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{3}{5}}{\frac{4}{5}}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．
点评 本题考查了同角三角函数关系，利用sin2α+cos2α=1，tanα=$\frac{sinα}{cosα}$是解题关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
4．
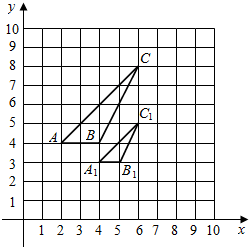如图，△ABC与△A1B1C1是位似图形，且顶点都在格点上，则位似中心坐标是（ ）
如图，△ABC与△A1B1C1是位似图形，且顶点都在格点上，则位似中心坐标是（ ）| A． | （6，2） | B． | （6，1） | C． | （4，2） | D． | （2，6） |
如图，在Rt△ABC中，已知∠C=90°，BC=5，AB=5$\sqrt{2}$，求∠A、∠B及AC的值．