题目内容
6. 如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.
如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.(1)求直线与抛物线的解析式;
(2)设抛物线的顶点为P,求△PCD的面积.
分析 (1)把点C的坐标(1,7)代入y=kx+5得到k的值,从而得到一次函数的解析式;把x=5代入y=2x+5,得y=15,得到D点坐标,把C(1,7)、D(5,15)代入y=ax2+bx,即可组成方程组求出抛物线的解析式;
(2)根据抛物线解析式求得点P的坐标,然后根据三角形的面积公式进行解答即可.
解答 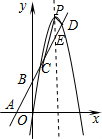 解:(1)把点C的坐标(1,7)代入y=kx+5得,7=k+5,
解:(1)把点C的坐标(1,7)代入y=kx+5得,7=k+5,
解得k=2,
∴y=2x+5,
把x=5代入y=2x+5,得y=15,
∴D(5,15).
把C(1,7)、D(5,15)代入y=ax2+bx,得a=-1,b=8,
∴y=-x2+8x;
(2)由(1)知,抛物线的解析式为y=-x2+8x=-(x-4)2+16,则顶点P(4,16).
则对称轴为x=4.
设x=4与直线CD交于点E.
又C(1,7)、D(5,15),
∴直线CD的解析式为:y=2x+5.
把x=4代入得到:y=2×4+5=13,
∴E(4,13),
∴PE=3.
故S△PCD=$\frac{1}{2}$×3×4=6.
点评 本题考查了待定系数法求二次函数解析式,二次函数与一次函数交点问题.求函数解析式的过程就是一个列代数式的过程,求线段的长度的问题一般要转化为求点的坐标的问题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
17.下列计算中正确的是( )
| A. | (x-1)-2=x2 | B. | x2n÷x2=xn(n是正整数) | ||
| C. | (-2x2)3=-6x6 | D. | (-3a-2)(3a-2)=9a2-4 |
15.去年体育测试中,从某校初三(1)班中抽取男、女生各15名进行三项体育成绩复查测试,在这个问题中,下列叙述正确的是( )
| A. | 该校所有初三学生是总体 | |
| B. | 所抽取的30名学生是样本 | |
| C. | 所抽取的15名学生是样本 | |
| D. | 所抽取的30名学生的体育成绩是样本 |