题目内容
(1)已知
=
=
,求
的值.
(2)已知∠A,∠B,∠C是锐角△ABC的三个内角,且满足(2sinA-
)2+
=0,求∠C的度数.
| a |
| 3 |
| b |
| 5 |
| c |
| 7 |
| a+b-2c |
| b+c |
(2)已知∠A,∠B,∠C是锐角△ABC的三个内角,且满足(2sinA-
| 3 |
| tanB-1 |
考点:特殊角的三角函数值,非负数的性质:偶次方,非负数的性质:算术平方根,比例的性质
专题:
分析:(1)首先设
=
=
=k,则可得a=3k,b=5k,c=7k,然后将其代入
,即可求得答案;
(2)根据非负数的性质可得sinA=
,tanB=1,根据sinA=
,∠A是锐角,可知∠A=60°,同理可得∠B=45°,结合三角形内角和定理可求∠C.
| a |
| 3 |
| b |
| 5 |
| c |
| 7 |
| a+b-2c |
| b+c |
(2)根据非负数的性质可得sinA=
| ||
| 2 |
| ||
| 2 |
解答:解:(1)设
=
=
=k,则a=3k,b=5k,c=7k,
=
=-
;
(2)由(2sinA-
)2+
=0得sinA=
,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=75°.
| a |
| 3 |
| b |
| 5 |
| c |
| 7 |
| a+b-2c |
| b+c |
=
| 3k+5k-14k |
| 5k+7k |
=-
| 1 |
| 2 |
(2)由(2sinA-
| 3 |
| tanB-1 |
| ||
| 2 |
∴∠A=60°,∠B=45°,
∴∠C=180°-∠A-∠B=75°.
点评:此题考查了比例的性质.此题难度不大,注意掌握设
=
=
=k的解题方法.同时考查了特殊三角函数值、三角形内角和定理,解题的关键是熟练掌握30°、60°、45°这些特殊角的特殊三角函数值.
| a |
| 3 |
| b |
| 5 |
| c |
| 7 |

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知x=2-
,则x2-4x-7的值为( )
| 3 |
| A、7 | B、8 | C、-7 | D、-8 |
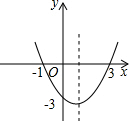 已知二次函数的图象如图,则这个二次函数的表达式为
已知二次函数的图象如图,则这个二次函数的表达式为 已知,如图,?ABCD的对角线AC、BD相交于点O,过O的直线EF分别于边AB、DC相交于点E、F.
已知,如图,?ABCD的对角线AC、BD相交于点O,过O的直线EF分别于边AB、DC相交于点E、F.