题目内容
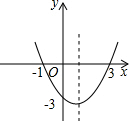已知二次函数的图象如图，则这个二次函数的表达式为考点：待定系数法求二次函数解析式
专题：计算题
分析：根据图象设出抛物线的两根形式y=a（x+1）（x-3），将（0，-3）代入求出a的值，即可确定出解析式．
解答：解：根据图象设抛物线解析式为y=a（x+1）（x-3），
将（0，-3）代入解析式得：-3=-3a，即a=1，
则抛物线解析式为y=（x+1）（x-3）=x2-2x-3．
故答案为：y=x2-2x-3．
将（0，-3）代入解析式得：-3=-3a，即a=1，
则抛物线解析式为y=（x+1）（x-3）=x2-2x-3．
故答案为：y=x2-2x-3．
点评：此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
下列式子中二次根式有（ ）
；
；
；
（x≤3）；
；
．
| 3 |
| (-5)2 |
| 3 | 13 |
| 3-x |
| -x2-5 |
| (x-1)2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，在平面直角坐标系中，点A的坐标为（-1，0），点B的坐标为（0，2），以点A为中心，将线段AB逆时针旋转90°，则点B的对应点B′的坐标是