题目内容
17.若$\frac{a+b}{c}$=$\frac{c+b}{a}$=$\frac{a+c}{b}$,求$\frac{(a+b)(c+b)(a+c)}{abc}$的值.分析 首先设$\frac{a+b}{c}$=$\frac{c+b}{a}$=$\frac{a+c}{b}$=K得出(b+c)+(c+a)+(a+b)=K(a+b+c),进而求出K的值,再分别代入原式求出答案.
解答 解:设$\frac{a+b}{c}$=$\frac{c+b}{a}$=$\frac{a+c}{b}$=K,
则b+c=aK(1),
c+a=bK(2),
a+b=cK(3),
则(1)+(2)+(3),
(b+c)+(c+a)+(a+b)=K(a+b+c),
2(a+b+c)=K(a+b+c),
K(a+b+c)-2(a+b+c)=0,
(K-2)(a+b+c)=0,
解得:K=2 或a+b+c=0,
当K=2时,$\frac{(a+b)(c+b)(a+c)}{abc}$=$\frac{abc{K}^{3}}{abc}$=8,
当a+b+c=0时,a+b=-c,b+c=-a,a+c=-b,
$\frac{(a+b)(c+b)(a+c)}{abc}$=-1
故原式有两个解:8或-1.
点评 此题主要考查了分式的化简求值,根据题意得出$\frac{a+b}{c}$=$\frac{c+b}{a}$=$\frac{a+c}{b}$的值是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
5.设M=14+24+34+…+20134+20144,则M的个位数字为( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
4.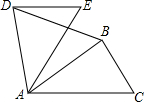 如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
 如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |

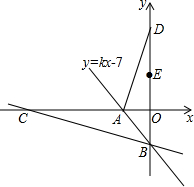 将直角坐标系中一次函数的图象与坐标轴围成三角形,叫做此一次函数的坐标三角形(也称为直线的坐标三角形).如图,一次函数y=kx-7的图象与x,y轴分别交于点A,B,那么△ABO为此一次函数的坐标三角形(也称直线AB的坐标三角形).
将直角坐标系中一次函数的图象与坐标轴围成三角形,叫做此一次函数的坐标三角形(也称为直线的坐标三角形).如图,一次函数y=kx-7的图象与x,y轴分别交于点A,B,那么△ABO为此一次函数的坐标三角形(也称直线AB的坐标三角形).