题目内容
如图,边长为a的菱形ABCD中,∠A=60°,过C任作直线分别交AB、AD的延长线于E、F,连接DE、BF交于M,若△BEM和△DFM外接圆的半径分别是R1、R2,求证:R1•R2为定值,并求这个定值.
【答案】分析:可以证明△BEC∽△DCF,证得∠ABD=60°,根据正弦定理就可以求出.
解答:证明: △BEC∽△DCF,
△BEC∽△DCF,
 ∴
∴ .
.
∴△BED∽△DBF.
∴∠BED=∠DBM.
∴∠BME=∠BDM+∠DBM=∠BDM+∠BED=∠ABD=60°.
∴由正弦定理得:2R1= ,2R2=
,2R2= .
.
∴R1•R2= •
• =
= =
= .
.
点评:本题主要考查了相似三角形的性质以及正弦定理的运用.
解答:证明:
 △BEC∽△DCF,
△BEC∽△DCF, ∴
∴ .
.∴△BED∽△DBF.
∴∠BED=∠DBM.
∴∠BME=∠BDM+∠DBM=∠BDM+∠BED=∠ABD=60°.
∴由正弦定理得:2R1=
 ,2R2=
,2R2= .
.∴R1•R2=
 •
• =
= =
= .
.点评:本题主要考查了相似三角形的性质以及正弦定理的运用.

练习册系列答案
相关题目
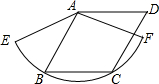 如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
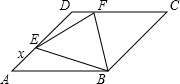 如图,边长为4的菱形ABCD中,∠DAB=60°,E是AD上的动点(与A,D不重合),F是CD上的动点,且AE+CF=4.
如图,边长为4的菱形ABCD中,∠DAB=60°,E是AD上的动点(与A,D不重合),F是CD上的动点,且AE+CF=4. 如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为
如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为 (2012•普陀区二模)如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上时,弧BC的长度等于
(2012•普陀区二模)如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上时,弧BC的长度等于 (2013•牡丹江)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是
(2013•牡丹江)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是