题目内容
（2013•牡丹江）如图，边长为1的菱形ABCD中，∠DAB=60°．连结对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°．连结AE，再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是（
）n-1
| 3 |
（
）n-1
．| 3 |
分析：连接DB于AC相交于M，根据已知和菱形的性质可分别求得AC，AE，AG的长，从而可发现规律根据规律不难求得第n个菱形的边长．
解答：
解：连接DB，
∵四边形ABCD是菱形，
∴AD=AB．AC⊥DB，
∵∠DAB=60°，
∴△ADB是等边三角形，
∴DB=AD=1，
∴BM=
，
∴AM=
，
∴AC=
，
同理可得AE=
AC=（
）2，AG=
AE=3
=（
）3，
按此规律所作的第n个菱形的边长为（
）n-1，
故答案为（
）n-1．
解：连接DB，∵四边形ABCD是菱形，
∴AD=AB．AC⊥DB，
∵∠DAB=60°，
∴△ADB是等边三角形，
∴DB=AD=1，
∴BM=
| 1 |
| 2 |
∴AM=
| ||
| 2 |
∴AC=
| 3 |
同理可得AE=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
按此规律所作的第n个菱形的边长为（
| 3 |
故答案为（
| 3 |
点评：此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力．
练习册系列答案
习题精选系列答案
相关题目
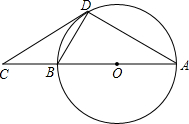（2013•牡丹江）如图，点C是⊙O的直径AB延长线上的一点，且有BO=BD=BC．