题目内容
20.设a、b是方程x2+3x+1=0的两实根,则代数式$\frac{1}{a^2}+\frac{1}{b^2}$的值为( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
分析 根据根与系数的关系得到a+b=-3,ab=1,再利用通分和完全平方公式得到原式=$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得a+b=-3,ab=1,
所以$\frac{1}{a^2}+\frac{1}{b^2}$=$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{(a+b)^{2}-2ab}{(ab)^{2}}$=$\frac{(-3)^{2}-2×1}{1}$=7.
故选B.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
4.抛物线y=ax2+bx+c经过点A(-1,2),B(1,-2),则b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
8.由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
| x | 1.0 | 1.1 | 1.2 | 1.3 |
| x2+12x | 13 | 14.41 | 15.84 | 17.29 |
| A. | 1.0<x<1.1 | B. | 1.1<x<1.2 | C. | 1.2<x<1.3 | D. | 14.41<x<15.84 |
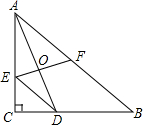 在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.
在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.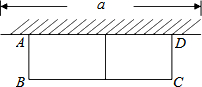 已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.则S与x的函数关系式s=-3x2+24x;自变量的取值范围$\frac{14}{3}$≤x<8.
已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.则S与x的函数关系式s=-3x2+24x;自变量的取值范围$\frac{14}{3}$≤x<8.