题目内容
 如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )
如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )| A、25° | B、20° |
| C、15° | D、10° |
考点:旋转的性质
专题:
分析:根据三角形的内角和定理求出∠ACB,再根据旋转的性质可得AC=AC1,∠AC1B1=∠ACB,然后求出∠AC1C,最后根据∠CC1B1=∠AC1C-∠AC1B1进行计算即可得解.
解答:解:∵∠BAC=90°,∠ABC=65°,
∴∠ACB=90°-65°=25°,
∵△AB1C1由△ABC绕点A顺时针旋转90°得到,
∴AC=AC1,∠AC1B1=∠ACB,
∴∠AC1C=45°,
∴∠CC1B1=∠AC1C-∠AC1B1=45°-25°=20°.
故选B.
∴∠ACB=90°-65°=25°,
∵△AB1C1由△ABC绕点A顺时针旋转90°得到,
∴AC=AC1,∠AC1B1=∠ACB,
∴∠AC1C=45°,
∴∠CC1B1=∠AC1C-∠AC1B1=45°-25°=20°.
故选B.
点评:本题考查了旋转的性质,等腰直角三角形的性质,熟记各性质并求出∠AC1C=45°是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,它们是一个物体的三视图,该物体的形状是( )
如图,它们是一个物体的三视图,该物体的形状是( )A、 |
B、 |
C、 |
D、 |
 如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )
如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )| A、4cm | ||
| B、8cm | ||
C、2
| ||
| D、6cm |
 如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.
如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.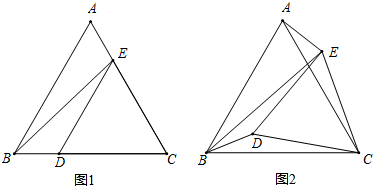 已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.
已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.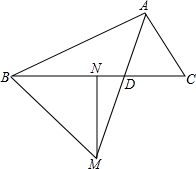 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°. 画出如图立体图形的三视图.
画出如图立体图形的三视图.