题目内容
12．当1＜x＜2时，化简：$\sqrt{（x-2）^{2}}$+$\sqrt{{x}^{2}-2x+1}$的结果为1．分析 根据x的取值范围得出x-2＜0，x-1＞0，进而化简求出即可．
解答 解：当1＜x＜2时，x-2＜0，x-1＞0，
$\sqrt{（x-2）^{2}}$+$\sqrt{{x}^{2}-2x+1}$
=2-x+x-1
=1．
故答案为：1．
点评 此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
2．已知样本数据1、2、2、3、7，下列说法不正确的是（ ）
| A． | 平均数是3 | B． | 中位数是2 | C． | 方差是2 | D． | 众数是2 |
3．如图中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
20．某次歌咏比赛，最后三名选手的成绩统计如下：
若唱功，音乐常识，综合知识按6：3：1的加权平均分排出冠军、亚军、季军、则冠军，亚军，季军分别是
（ ）
| 测试项目 | 测试成绩 | ||
| 王飞 | 李真 | 林杨 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
（ ）
| A． | 王飞、李真、林杨 | B． | 李真、王飞、林杨 | C． | 王飞、林杨、李真 | D． | 李真、林杨、王飞 |
7．下列命题中正确的个数是（ ）
①垂直于弦的直径平分线以及弦所对的两条弧．②平分弦的直径垂直于这条弦，并且平分这条弦所对的两条弧．③弦的垂直平分线经过圆心，并且平分这条弦所对的两条弦．④平分弦所对的一条弧的直径垂直平分这条弦，并且平分这条弦所对的另一条弧．
①垂直于弦的直径平分线以及弦所对的两条弧．②平分弦的直径垂直于这条弦，并且平分这条弦所对的两条弧．③弦的垂直平分线经过圆心，并且平分这条弦所对的两条弦．④平分弦所对的一条弧的直径垂直平分这条弦，并且平分这条弦所对的另一条弧．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
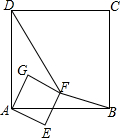正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图．
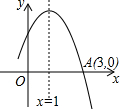如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），对称轴为x=1，给出四个结论：①b2-4ac＞0；②2a+b=0；③a+b=0；④当x=-1或x=3时，函数y的值都等于0，其中正确结论是（ ）
已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．