题目内容
15.先化简,再求代数式$\frac{5a+4b}{{a}^{2}-{b}^{2}}-\frac{3b+4a}{{a}^{2}-{b}^{2}}$的值,其中a=2cos30°,b=2tan45°.分析 先根据分式混合运算的法则把原式进行化简,再求出a,b的值代入进行计算即可.
解答 解:原式=$\frac{5a+4b-3b-4a}{(a+b)(a-b)}$
=$\frac{1}{a-b}$,
∵a=2cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,b=2tan45°=2,
∴原式=$\frac{1}{\sqrt{3}-2}$=-$\sqrt{3}$-2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
5.已知一个半径为6的扇形面积是4π,则这个扇形的圆心角是( )
| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
3.如图中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.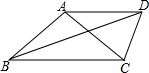 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
20.某次歌咏比赛,最后三名选手的成绩统计如下:
若唱功,音乐常识,综合知识按6:3:1的加权平均分排出冠军、亚军、季军、则冠军,亚军,季军分别是
( )
| 测试项目 | 测试成绩 | ||
| 王飞 | 李真 | 林杨 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
( )
| A. | 王飞、李真、林杨 | B. | 李真、王飞、林杨 | C. | 王飞、林杨、李真 | D. | 李真、林杨、王飞 |
7.下列命题中正确的个数是( )
①垂直于弦的直径平分线以及弦所对的两条弧.②平分弦的直径垂直于这条弦,并且平分这条弦所对的两条弧.③弦的垂直平分线经过圆心,并且平分这条弦所对的两条弦.④平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧.
①垂直于弦的直径平分线以及弦所对的两条弧.②平分弦的直径垂直于这条弦,并且平分这条弦所对的两条弧.③弦的垂直平分线经过圆心,并且平分这条弦所对的两条弦.④平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.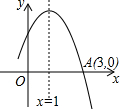 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
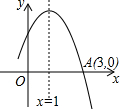 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )| A. | ②③④ | B. | ①③④ | C. | ①②③ | D. | ①②④ |
5. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |