Question

2．在同一平面直角坐标系内画出函数y₁=$\frac{1}{2}$x-2和y₂=-x+1的图象，并回答下列问题：
（1）方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{y=-x+1}\end{array}\right.$的解是什么？
（2）x为何值时，y₁＞y₂？x为何值时，y₁＜y₂？

Answer 1

分析 （1）利用函数图象性质，求出两条直线与x轴、y轴的交点，画出图象，两条直线的交点即为方程组的解；
（2）分析函数图象，观察图象位置关系，图象在上面，函数值就大，即可得出答案．

解答 解：（1）令函数y₁=$\frac{1}{2}$x-2，x=0，解得y=-2，
y=0，解得x=4，
∴函数过（0，2），（4，0）；
令函数y₂=-x+1，x=0，解得y=1，
y=0，解得x=1，
∴函数过（0，1），（1，0）；
画出图象如下：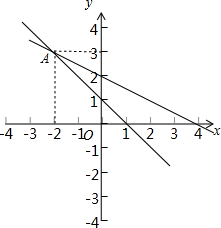

通过观察，两条直线交于点A（-2，3），
∴方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{y=-x+1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$．

（2）由（1）凸显观察：
当x＞-2时，y₁＞y₂．
当x＜-2时，y₁＜y₂．

点评 题目考查了一次函数与二元一次方程组及一次函数与一元一次不等式的关系，解决此类题目的关键是掌握数形结合法，题目整体难易程度适中，适合课后训练．