题目内容
7.在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′(点A的对应点为点A′),若点A′的坐标为(-3,2),则点B′的坐标为( )| A. | (4,3) | B. | (2,4) | C. | (-1,-2) | D. | (-2,-1) |
分析 根据点A到A′确定出平移规律,再根据平移规律列式计算即可得到点B′的坐标.
解答 解:∵A(-4,-1),A′(-3,2),
∴平移规律为横坐标加1,纵坐标加3,
∵B(1,1),
∴1+1=2,1+3=4,
∴点B′的坐标为(2,4).
故选B.
点评 本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,先确定出平移规律是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.若关于x的不等式(2-m)x≤m-2的解集为x≥-1,则m应满足的条件是( )
| A. | m>0 | B. | m<2 | C. | m≥2 | D. | m>2 |
18.如果∠A与∠B的两边互相垂直,则∠A与∠B的关系为( )
| A. | ∠A=∠B | B. | ∠A+∠B=90° | ||
| C. | ∠A+∠B=180° | D. | ∠A=∠B或∠A+∠B=180° |
15.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AD=BC |
2.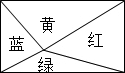 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )| A. | 60cm2 | B. | 70cm2 | C. | 120cm2 | D. | 140cm2 |
19. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )| A. | 44° | B. | 60° | C. | 67° | D. | 70° |
 已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.
已知:如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=24°,求∠ABE的度数.