��Ŀ����
3�������ۡ���֪����ֱ��L1��y=k1x+b1��L2��k2x+b2����L1��L2������k1•k2=-1����֮Ҳ��������Ӧ�á���1����֪y=3x+1��y=kx-1��ֱ����k�����ǵĽ������ꣻ
��2����ֱ֪��M������A��2��3��������y=-$\frac{1}{2}$x+3��ֱ����ֱ��M�Ľ���ʽ��
��̽������3����ͬһֱ������ϵ�ϣ�����4����A��1��3����B��-3��0����C��0��-4����D��4��-1���������������������ܵõ���������ͬ��ֱ�ߣ���Щֱ���й��ж����黥�ഹֱ��ϵ����ѡ������һ�黥�ഹֱ��ϵ����֤����
���� ��1���������еĽ�����3k=-1����ɽ��k=-$\frac{1}{3}$��Ȼ��ͨ��������$\left\{\begin{array}{l}{y=3x+1}\\{y=-\frac{1}{3}x-1}\end{array}\right.$�����ǵĽ������ꣻ
��2���������еĽ�����ֱ��M�Ľ���ʽ��һ����ϵ��Ϊ2����ֱ��M�Ľ���ʽ����Ϊy=2x+b��Ȼ���A������������b���ɣ�
��3������ȷ��һֱ�ߣ�������ϵ��������㣬���ɵõ��������������ܵõ�6����ͬ��ֱ�ߣ���Щֱ���й���5�黥�ഹֱ��ϵ����ѡȡһ�鴹ֱ��ϵ����֤���������ô���ϵ���������ֱ�ߵĽ���ʽ��Ȼ��������еĽ����ж���ֱ���Ƿ�ֱ��
��� �⣺��1����y=3x+1��y=kx-1��ֱ��
��3k=-1��
��k=-$\frac{1}{3}$��
�ⷽ����$\left\{\begin{array}{l}{y=3x+1}\\{y=-\frac{1}{3}x-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{3}{5}}\\{y=-\frac{4}{5}}\end{array}\right.$��
�����ǵĽ�������Ϊ��-$\frac{3}{5}$��-$\frac{4}{5}$����
��2���߹���Aֱ����y=-$\frac{1}{2}$x+3��ֱ��
�������Aֱ�ߵ�ֱ�߽���ʽΪy=2x+b��
��A��2��3������ã�b=-1��
�����ʽΪy=2x-1��
��3�������������������ܵõ�6��ֱ�ߣ���Щֱ���й���5�黥�ഹֱ��ϵ�����Ƿֱ��ǣ�AB��BC��BC��CD��CD��DA��DA��AB��AC��BD��
��ֱ��BCΪ��y=mx-4��
��B��-3��0�������0=-3m-4�����m=-$\frac{4}{3}$��
��ֱ��CDΪ��y=nx-4��
��D��4��-1������ã�-1=4n-4�����n=$\frac{3}{4}$��
��mn=-$\frac{4}{3}$��$\frac{3}{4}$=-1��
��BC��CD��
���� ���⿼������ֱ���ཻ��ƽ�����⣺����ֱ�ߵĽ������꣬������������ֱ�����Ӧ��һ�κ�������ʽ����ɵĶ�Ԫһ�η�����Ľ⣻������ֱ����ƽ�еĹ�ϵ����ô���ǵ��Ա���ϵ����ͬ����kֵ��ͬ��Ҳ�������¶��壮

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�| ��Ŀ ��Ա | �Ķ� | ˼ά | ���� |
| �� | 93 | 86 | 73 |
| �� | 95 | 81 | 79 |
��2������ʵ����Ҫ����˾���Ķ���˼ά�ͱ�������������Ե÷ְ�3��5��2�ı�ȷ��ÿ�˵����ɼ��������˳ɼ��ڼס���������¼��һ�ˣ�˭����¼�ã�
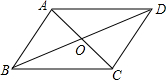 ?ABCD�У��Խ���AC��BD���ڵ�O����DAC=42�㣬��CBD=23�㣬���COD�ǣ�������
?ABCD�У��Խ���AC��BD���ڵ�O����DAC=42�㣬��CBD=23�㣬���COD�ǣ�������| A�� | 61�� | B�� | 63�� | C�� | 65�� | D�� | 67�� |