题目内容
12.解下列不等式(组):(1)解不等式:$\frac{x-1}{3}$≤5-x;
(2)解不等式组:$\left\{\begin{array}{l}{x+3>1}\\{x+2(x-1)≤1}\end{array}\right.$.
分析 (1)去分母、去括号、然后移项、合并同类项,系数化成1即可求解;
(2)首先解两个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)去分母,得x-1≤3(5-x)
去括号,得x-1≤15-3x,
移项,得:x+3x≤15+1,
合并同类项,得:4x≤16,
系数化成1得:x≤4;
(2)$\left\{\begin{array}{l}{x+3>1…①}\\{x+2(x-1)≤1…②}\end{array}\right.$,
解①得:x>-2,
解②得:x≤1.
则不等式组的解集是:-2<x≤1.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
20. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )| A. | 90° | B. | 360° | C. | 180° | D. | 540° |
17.下列命题的真命题是( )
| A. | 相等的角不一定是对顶角 | B. | 非正数没有平方根 | ||
| C. | 内错角相等 | D. | 和为180°的两个角一定是邻补角 |
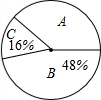 某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有18人.
某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有18人. 如图所示,已知∠1=52°,∠2=52°,∠3=91°,那么∠4=89.
如图所示,已知∠1=52°,∠2=52°,∠3=91°,那么∠4=89.