题目内容
6.已知关于x的方程x2-4x+3a-1=0有两个实数根.(1)求实数a的取值范围;
(2)若a为正整数,求方程x2-4x+3a-1=7的值.
分析 (1)利用判别式的意义得到△=(-4)2-4(3a-1)≥0,然后不等式即可;
(2)先确定a的值,然后利用因式分解法解方程即可.
解答 解:(1)根据题意得△=(-4)2-4(3a-1)≥0,
解得a≤$\frac{5}{3}$;
(2)∵a为正整数,
∴a=1,
∴方程化为x2-4x+2=7,
整理得x2-4x-5=0,
解得x1=5,x2=-1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
17.以下各数$\frac{22}{7}$,3.14159265,$\sqrt{7}$,-8,$\root{3}{2}$,0.6060060006…,0,$\sqrt{36}$,$\frac{π}{3}$,无理数的个数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
1.△ABC∽△DEF,且它们的周长之比为2:3,则它们的面积之比为( )
| A. | 2:3 | B. | 4:6 | C. | 4:9 | D. | 3:2 |
18.既是方程2x-y=3的解,又是方程3x-4y=2的解的是( )
| A. | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-5\end{array}\right.$ |
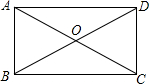 如图,在矩形ABCD中,AB=5cm,且∠BOC=120°,则AC的长为10cm.
如图,在矩形ABCD中,AB=5cm,且∠BOC=120°,则AC的长为10cm.