题目内容
7.阅读理解:将一个正整数分成若干个连续整数的和.例:①15=3×5 15=4+5+6 或15=1+2+3+4+5
②10=5×2 10=1+2+3+4
③8=2×2×2(无奇因数) 8不能拆分成若干个连续整数之和
试将下列各整数进行拆分:
①2005 ②2008 ③64.
分析 根据题意可知,将数字分解质因数,若含奇因数则可拆分成若干个连续整数之和,否则不能拆分,此题得解.
解答 解:根据题意可知,将已知数分解质因数,若含奇因数则可拆分成若干个连续整数之和,否则不能拆分.
①∵2005=5×401,
∴2005=399+400+401+402+403,
②∵2008=2×2×2×251,
2008=1+2+3+…+61+62,
③∵64=2×2×2×2×2×2,
∴64不能拆分成若干个连续整数之和
点评 本题考查了分解质因数,解题的关键是会利用分解质因数来解决问题.

练习册系列答案
相关题目
2.(-$\frac{1}{2}$)2001(-2)2000(-1)1999的正确答案( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
12.下列各式的乘积结果不含根式的是( )
| A. | 2$\sqrt{5}$×$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{2}$ | C. | ($\sqrt{3}$+$\sqrt{2}$)×$[-(\sqrt{3}+\sqrt{2})]$ | D. | $\sqrt{3a-4b}•\sqrt{3a+4b}$ |
16. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
 如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )| A. | S△CMN=$\frac{1}{2}$S△ABC | B. | CM:CA=1:2 | C. | MN∥AB | D. | AB=24m |
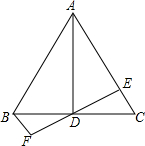 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AC于点E,BF⊥DE于点F
如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AC于点E,BF⊥DE于点F 如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.
如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.