题目内容
16.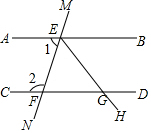 如图,直线AB与直线CD被直线MN所截,交点分别为点E、F,∠BEF的平分线EH交CD于点G,且∠1+∠2=180°.
如图,直线AB与直线CD被直线MN所截,交点分别为点E、F,∠BEF的平分线EH交CD于点G,且∠1+∠2=180°.(1)求证:∠FEG=∠FGE;
(2)若∠1=$\frac{1}{2}$∠2,求∠FGE的度数,并写出图中与∠1相等的角.
分析 (1)根据平行线的判定得出AB∥CD,根据平行线的性质得出∠BEH=∠FGE,根据角平分线定义得出∠BEH=∠FEG,即可求出答案;
(2)求出∠1=60°,∠BEG+∠FEG=120°,根据角平分线定义求出∠BEG=∠FEG=60°,即可求出答案.
解答 (1)证明:∵∠1+∠2=180°,
∴AB∥CD,
∴∠BEH=∠FGE,
∵∠BEF的平分线EG,
∴∠BEH=∠FEG,
∴∠FEG=∠FGE;
(2)解:∵∠1+∠2=180°,∠1=$\frac{1}{2}∠2$,
∴∠1=60°,
∴∠BEG+∠FEG=180°-60°=120°,
∵∠BEG=∠FEG,
∴∠BEG=∠FEG=60°,
∵∠FEG=∠FGE,
∴∠FGE=60°,
图中与∠1相等的角有∠MEB、∠BEG、∠FEG,∠FGE,∠CFN,∠DGH,∠EFG,共7个
点评 本题考查了平行线的性质和判定,角平分线定义等知识点,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1. 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
8.下列说法正确的是( )
| A. | 如果一件事发生的机会只有千万分之一,那么它就是不可能事件 | |
| B. | 如果一件事发生的机会达99.999%,那么它就是必然事件 | |
| C. | 如果一件事不是不可能事件,那么它就是必然事件 | |
| D. | 如果一件事不是必然事件,那么它就是不可能事件或随机事件 |
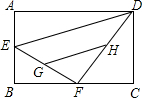 如图,在矩形ABCD中,AB=4,AD=6,点E是AB的中点,点F是BC边上的动点,连接EF,DF,G,H分别是EF和DF的中点,则GH的长为$\sqrt{10}$.
如图,在矩形ABCD中,AB=4,AD=6,点E是AB的中点,点F是BC边上的动点,连接EF,DF,G,H分别是EF和DF的中点,则GH的长为$\sqrt{10}$.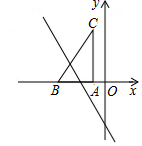 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度.
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度. 如图:∠A=40°,∠B=24°,把△ABC绕点C按顺时针方向旋转到△AB′C′,使点B′在AC的延长线上,则△ABC旋转了64度.
如图:∠A=40°,∠B=24°,把△ABC绕点C按顺时针方向旋转到△AB′C′,使点B′在AC的延长线上,则△ABC旋转了64度.