题目内容
5.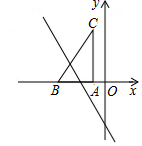 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度.
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度.
分析 利用勾股定理求出点C的坐标,再利用一次函数图象上点的坐标特征求出点C平移后得到新点的坐标,由此即可得出结论.
解答 解:在Rt△ABC中,AB=-1-(-4)=3,BC=5,
∴AC=$\sqrt{B{C}^{2}-A{C}^{2}}$=4,
∴点C的坐标为(-1,4).
当y=-2x-6=4时,x=-5,
-1-(-5)=4,
∴点C沿x轴向左平移4个单位长度才能落在直线y=-2x-6上.
故答案为:4.
点评 本题考查了一次函数图象上点的坐标特征、坐标与图形变化中的平移以及勾股定理,利用勾股定理以及一次函数图象上点的坐标特征求出点C的坐标以及点C平移后得到新点的坐标是解题的关键.

练习册系列答案
相关题目
17.下列定理中逆命题是假命题的是( )
| A. | 直角三角形两条直角边的平方和等于斜边的平方 | |
| B. | 在一个三角形中,如果两边相等,那么它们所对的角也相等 | |
| C. | 同位角相等,两直线平行 | |
| D. | 全等三角形的对应角相等 |
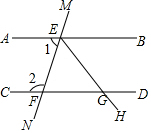 如图,直线AB与直线CD被直线MN所截,交点分别为点E、F,∠BEF的平分线EH交CD于点G,且∠1+∠2=180°.
如图,直线AB与直线CD被直线MN所截,交点分别为点E、F,∠BEF的平分线EH交CD于点G,且∠1+∠2=180°.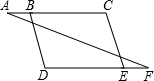 完成下面的证明(在括号中填写推理理由)
完成下面的证明(在括号中填写推理理由)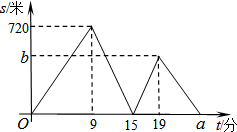 小文,小亮从学校出发到青少年宫参加书法比赛,小文步行一时间后,小亮骑自行车沿相同路线行走,两人均匀速前行,他们的路程差s(米)与小文出发时间t(分)之间的关系如图所示.
小文,小亮从学校出发到青少年宫参加书法比赛,小文步行一时间后,小亮骑自行车沿相同路线行走,两人均匀速前行,他们的路程差s(米)与小文出发时间t(分)之间的关系如图所示. 如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时.
如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时.