题目内容
11.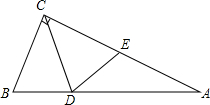 如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
分析 首先过点D作DN⊥AC于N,过点D作DM⊥AB,由折叠的性质可得:∠BCD=∠ACD,CE=CB=3,由角平分线的性质,可得DM=DN,然后利用三角形的面积,即可求得答案.
解答 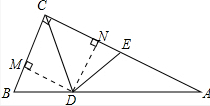 解:过点D作DN⊥AC于N,过点D作DM⊥AB,
解:过点D作DN⊥AC于N,过点D作DM⊥AB,
由折叠的性质可得:∠BCD=∠ACD,CE=CB=3,
∴DM=DN,
∵E是AC的中点,
∴AC=2AE=6,
∵S△BAC=S△BCD+S△ACD,
即$\frac{1}{2}$CB•AC=$\frac{1}{2}$BC•DM+$\frac{1}{2}$AC•DN,
∴$\frac{1}{2}$×3×6=$\frac{1}{2}$×DN×3+$\frac{1}{2}$×6×DN,
解得:DN=2,
∴点D到AC的距离是2.
故答案为:2.
点评 此题考查了折叠的性质以及三角形面积问题,注意掌握辅助线的作法是解此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )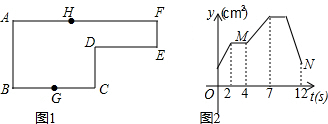
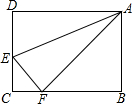 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.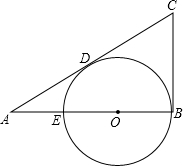 如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根.
如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根.