题目内容
5.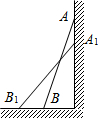 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC-AA1=$\sqrt{{2.5}^{2}-{0.7}^{2}}$-0.4=2
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程(x+0.7)2+22=2.52,
解方程得x1=0.8,x2=-2.2(不合题意舍去),∴点B将向外移动0.8米.
(2)解完“思考题”后,小聪提出了如下问题:
梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?请你解答小聪提出的这个问题.
分析 (1)设点B将向外移动x米,即BB1=x,B1C=x+0.7,根据勾股定理求出A1C=AC-AA1=$\sqrt{{2.5}^{2}-{0.7}^{2}}$-0.4=2.在Rt△A1B1C中,由勾股定理得到B1C2+A1C2=A1B12,依此列出方程方程(x+0.7)2+22=2.52,解方程即可;
(2)设梯子顶端从A处下滑x米,点B向外也移动x米,根据勾股定理可得(x+0.7)2+(2.4-x)2=2.52,再解即可.
解答 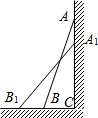 解:(1)设点B将向外移动x米,即BB1=x,
解:(1)设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC-AA1=$\sqrt{{2.5}^{2}-{0.7}^{2}}$-0.4=2.
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程(x+0.7)2+22=2.52,
解方程得x1=0.8,x2=-2.2(不合题意舍去),∴点B将向外移动0.8m.
故答案为(x+0.7)2+22=2.52,0.8,-2.2(不合题意舍去),0.8;
(2)有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+0.7)2+(2.4-x)2=2.52,
解得:x1=1.7或x2=0(不合题意舍去).
故当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
点评 本题主要考查了一元二次方程的应用及勾股定理的应用,根据题意得出关于x的一元二次方程是解答此题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
16.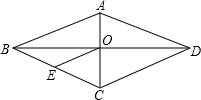 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
13.已知(m+n)2=5,mn=1,则m2+n2的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
10. 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )
 下图中能用一个字母表示的角( )
下图中能用一个字母表示的角( )| A. | 三个 | B. | 四个 | C. | 五个 | D. | 没有 |
17. 如图,下列表示角的方法,错误的是( )
如图,下列表示角的方法,错误的是( )
 如图,下列表示角的方法,错误的是( )
如图,下列表示角的方法,错误的是( )| A. | ∠1与∠AOB表示同一个角 | B. | ∠AOC也可用∠O来表示 | ||
| C. | 图中共有三个角:∠AOB、∠AOC、∠BOC | D. | ∠β表示的是∠BOC |
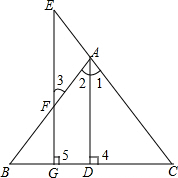 已知:如图,AD⊥BC于D,EG⊥BC于G,AD是∠BAC的角平分线,试说明∠E=∠3.
已知:如图,AD⊥BC于D,EG⊥BC于G,AD是∠BAC的角平分线,试说明∠E=∠3.