题目内容
13. (1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;
(1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;(2)在△ABC中,若AB=BC,则过其中一个顶点的一条直线,将△ABC分成两个等腰三角形,请直接写出△ABC顶角的度数.
分析 (1)过B作直线BE交AC于D.可以求出∠DBC和∠ADB的度数,从而求解;由于同一个三角形中内角不能存在两个钝角,反证法即可得出)∠A不能为另一等腰三角形的顶角,再根据等腰三角形的性质求解;
(2)因为题中没有指明是过顶角的顶点还是过底角的顶点,故应该分四情况进行分析,从而求解.
解答 解:(1)过B作直线BE交AC于D.
∵∠C为顶角,
∴∠DBC=∠CDB=$\frac{180°-40°}{2}$=70°,
∴∠ADB=110°,∠ABD=∠A=$\frac{180°-110°}{2}$=35°,
∴∠ABC=35°+70°=105°.
∵∠ADB=∠C+$\frac{180°-∠C}{2}$=90°+$\frac{1}{2}$∠C,
∴∠ADB为钝角,
又∵同一个三角形中内角不能存在两个钝角,
∴∠A不能为顶角.
当∠ADB为顶角时,∠ABC=∠ABD+∠DBC=$\frac{1}{2}$+∠DBC=$\frac{3}{2}$=135°-$\frac{3}{4}$∠C.
故答案为:105;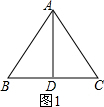
(2)①如图1,∵AB=AC,当BD=CD,CD=AD,
∴∠B=∠C=∠BAD=∠CAD,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠BAC=90°.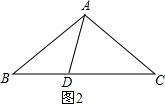
②如图2,∵AB=AC,AD=BD,AC=CD,
∴∠B=∠C=∠BAD,∠CAD=∠CDA,
∵∠CDA=∠B+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,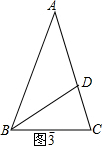
∴∠BAC=108°.
③如图3,∵AB=AC,AD=BD=BC,
∴∠B=∠C,∠BAC=∠ABD,∠BDC=∠C,
∵∠BDC=∠A+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠BAC=180°,
∴∠BAC=36°.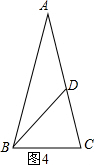
④如图4,∵AB=AC,AD=BD,CD=BC,
∴∠ABC=∠C,∠BAC=∠ABD,∠CDB=∠CBD,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠C=3∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴7∠BAC=180°,
∴∠BAC=($\frac{180}{7}$)°
点评 本题考查的是应用与设计作图及等腰三角形的性质,在解答此题时要注意进行分类讨论,不要漏解.

 开心快乐假期作业暑假作业西安出版社系列答案
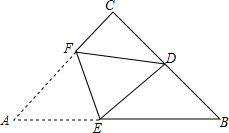
开心快乐假期作业暑假作业西安出版社系列答案 如图,将△ABC纸片折叠,使C落在三角形的内部,求证:∠ADC+∠BEC=2∠C.
如图,将△ABC纸片折叠,使C落在三角形的内部,求证:∠ADC+∠BEC=2∠C.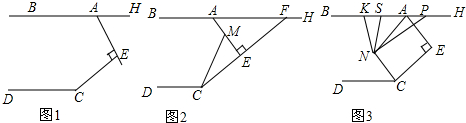
 如图,在等腰直角三角形ABC中,∠C=90°,点D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕.
如图,在等腰直角三角形ABC中,∠C=90°,点D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕. 如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,AD平分∠BAC,求证:AB=AC.
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,AD平分∠BAC,求证:AB=AC.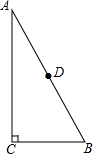 如图,在Rt△ABC中,∠C=90°,D是AB的中点.AC=4,BC=2,以C为圆心,$\sqrt{5}$为半径作⊙C,A,B,D三点与⊙C的位置关系如何.
如图,在Rt△ABC中,∠C=90°,D是AB的中点.AC=4,BC=2,以C为圆心,$\sqrt{5}$为半径作⊙C,A,B,D三点与⊙C的位置关系如何. 如图,要设计一本书的封面,封面长25cm,宽15cm.正中央是一个与整个封面长宽比例相同的矩形,如果要使四周边衬所占面积是封面面积的$\frac{9}{25}$,且上、下边衬等宽,左、右边衬等宽,则上下边衬的宽4.5cm.
如图,要设计一本书的封面,封面长25cm,宽15cm.正中央是一个与整个封面长宽比例相同的矩形,如果要使四周边衬所占面积是封面面积的$\frac{9}{25}$,且上、下边衬等宽,左、右边衬等宽,则上下边衬的宽4.5cm.