题目内容
2.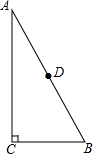 如图,在Rt△ABC中,∠C=90°,D是AB的中点.AC=4,BC=2,以C为圆心,$\sqrt{5}$为半径作⊙C,A,B,D三点与⊙C的位置关系如何.
如图,在Rt△ABC中,∠C=90°,D是AB的中点.AC=4,BC=2,以C为圆心,$\sqrt{5}$为半径作⊙C,A,B,D三点与⊙C的位置关系如何.
分析 连接CD,先根据勾股定理求出AB的长,根据直角三角形的性质得出CD的长,再把AC,CD,BC的长与$\sqrt{5}$相比较即可得出结论.
解答 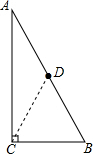 解:连接CD,
解:连接CD,
∵在Rt△ABC中,∠C=90°,AC=4,BC=2,
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
∵D是AB的中点,
∴CD=$\frac{1}{2}$AB=$\sqrt{5}$,
∴点D在⊙O上;
∵AC=4>$\sqrt{5}$,BC=2<$\sqrt{5}$,
∴点A在圆外,点B在圆内.
点评 本题考查的是点与圆的位置关系,根据题意作出辅助线,利用直角三角形的性质求出CD的长是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
14.当n为偶数时,(a-b)m•(b-a)n与(b-a)m+n的关系是( )
| A. | 相等 | |
| B. | 互为相反数 | |
| C. | 当m为偶数时互为相反数,当m为奇数时相等 | |
| D. | 当m为偶数时相等,当m为奇数时为互为相反数 |
 (1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;
(1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;