题目内容
13.抛物线y1=-2(x-4)2.(1)写出y1关于x轴对称的y2和关于y轴对称的y3的解析式;
(2)设y1与y轴交于点A,y2与y轴交于点B,y1与y3的顶点分别为点C、D,探索四边形ABCD的形状.
分析 (1)根据对称的性质求相关抛物线的解析式;
(2)根据抛物线解析式求得点A、B、C、D的坐标,由此求得相关线段的长度,易得到四边形ACBD是菱形.
解答 解:(1)y1关于x轴对称的y2的解析式为:y2=-y1=2(x-4)2,即y2=2(x-4)2.
y1关于y轴对称的y3的解析式为:y3=-2(-x-4)2,即y3=-2(x+4)2.
(2)由y2=2(x-4)2,y3=-2(x+4)2得到:A(0,-4$\sqrt{2}$),B(0,4$\sqrt{2}$),C(0,4),D(0,-4).
∴OA=OB,OC=OD,
∴四边形ACBD是平行四边形,
又AB⊥CD,
∴平行四边形ACBD是菱形.
点评 本题考查了二次函数图象与几何变换.解答(1)题时,也可以根据抛物线顶点的变换写出新抛物线的解析式.

练习册系列答案
相关题目
1.下列公式正确的是( )
| A. | a2=b2+c2+2bccosA | B. | a2=b2+c2+bccosA | ||
| C. | a2=b2+c2-2bccosA | D. | a2=b2+c2-2bcsinA |
 如图,已知线段AC=12cm,在线段AC上有一点B,且BC=4cm,M是线段AC的中点,求线段MB的长.
如图,已知线段AC=12cm,在线段AC上有一点B,且BC=4cm,M是线段AC的中点,求线段MB的长. 小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?
小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?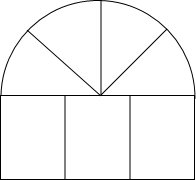 从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.
从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.