题目内容
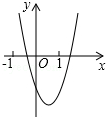已知二次函数y=ax2+bx+c（a，b，c是常数，且a≠0）的图象如图所示，则一次函数y=cx+| b |
| 2a |
| ab |
| x |
A、 |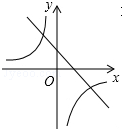
B、 |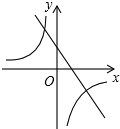
C、 |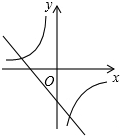
D、 |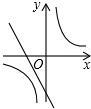
考点：二次函数图象与系数的关系,一次函数的图象,反比例函数的图象
专题：数形结合
分析：根据二次函数图象与系数的关系，由抛物线对称轴的位置确定ab＜0，由抛物线与y轴的交点位置确定c＜0，然后根据一次函数图象与系数的关系可判断一次函数经过第二、三、四象限，根据反比例函数的性质得到反比例函数图象在第二、四象限，由此可对各选项进行判断．
解答：解：∵抛物线对称轴在y轴右侧，
∴ab＜0，
∵抛物线与y轴的交点在x轴下方，
∴c＜0，
对于一次函数y=cx+
，c＜0，图象经过第二、四象限；
＜0，图象与y轴的交点在x轴下方；对于反比例函数y=
，ab＜0，图象分布在第二、四象限．
故选C．
∴ab＜0，
∵抛物线与y轴的交点在x轴下方，
∴c＜0，
对于一次函数y=cx+
| b |
| 2a |
| b |
| 2a |
| ab |
| x |
故选C．
点评：本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口，当a＜0时，抛物线向下；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）；常数项c决定抛物线与y轴交点．也考查了一次函数图象与反比例函数图象．
练习册系列答案
相关题目
若抛物线y=x2-2x+c与y轴的交点为（0，-3），则该抛物线与x轴的交点是（ ）
| A、（-1，0）和（0，3） |
| B、（0，-1）和（3，0） |
| C、（-1，0）和（3，0） |
| D、（0，-1）和（0，3） |
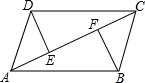如右图，已知DE⊥AC，BF⊥AC，垂足分别是E、F，AE=CF，DC∥AB，