题目内容
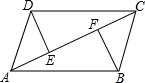 如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,(1)试证明:DE=BF;
(2)连接DF、BE,猜想DF与BE的关系?并证明你的猜想的正确性.
考点:全等三角形的判定与性质
专题:
分析:(1)求出AF=CE,∠AFB=∠DEC=90°,根据平行线的性质得出∠DCE=∠BAF,根据ASA推出△AFB≌△CED即可;
(2)根据平行四边形的判定得出四边形是平行四边形,再根据平行四边形的性质得出即可.
(2)根据平行四边形的判定得出四边形是平行四边形,再根据平行四边形的性质得出即可.
解答:(1)证明:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠DEC=90°,
∵DC∥AB,
∴∠DCE=∠BAF,
在△AFB和△CED中
∴△AFB≌△CED,
∴DE=EF;
(2)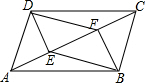
DF=BE,DF∥BE,
证明:∵DE⊥AC,BF⊥AC,
∴DE∥BF,
∵DE=BF,
∴四边形DEBF是平行四边形,
∴DF=BE,DF∥BE.
∴AE+EF=CF+EF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠DEC=90°,
∵DC∥AB,
∴∠DCE=∠BAF,
在△AFB和△CED中
|
∴△AFB≌△CED,
∴DE=EF;
(2)

DF=BE,DF∥BE,
证明:∵DE⊥AC,BF⊥AC,
∴DE∥BF,
∵DE=BF,
∴四边形DEBF是平行四边形,
∴DF=BE,DF∥BE.
点评:本题考查了全等三角形的性质和判定,平行线的性质,平行四边形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,五边形ABCDE关于直线l成轴对称的图形是五边形A1B1C1D1E1,下列说法中不正确的是( )
如图,五边形ABCDE关于直线l成轴对称的图形是五边形A1B1C1D1E1,下列说法中不正确的是( )| A、AB=A1B1 |
| B、BC∥B1C1 |
| C、直线l⊥BB1 |
| D、∠C=∠C1 |
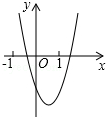 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+
 如图,直线y=-
如图,直线y=-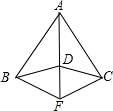 已知:如图,AB=AC,DB=DC.F是AD的延长线上一点.
已知:如图,AB=AC,DB=DC.F是AD的延长线上一点. 如图AB=AC,AD=AE,∠1=∠2,AB交CE于M,AC交BD于N,求证:AM=AN.
如图AB=AC,AD=AE,∠1=∠2,AB交CE于M,AC交BD于N,求证:AM=AN.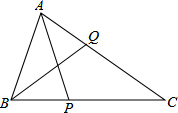 △ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.(有多种辅助线作法)
△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.(有多种辅助线作法) 如图,BD是圆O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.
如图,BD是圆O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.