题目内容
20.计算:(1)$\frac{2x-y}{x}-\frac{y}{y-2x}$;
(2)(-12x2y)2÷(-$\frac{3{x}^{2}}{y}$)2
(3)$\frac{2x-4}{{x}^{2}+3}÷\frac{x-2}{{x}^{2}+6x+9}$.
分析 (1)原式变形后,通分并利用同分母分式的加法法则计算即可得到结果;
(2)原式先计算乘方运算,再计算除法运算即可得到结果;
(3)原式利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{(2x-y)^{2}+xy}{x(2x-y)}$=$\frac{4{x}^{2}-3xy+{y}^{2}}{2{x}^{2}-xy}$;
(2)原式=144x4y2•$\frac{{y}^{2}}{9{x}^{4}}$=$\frac{144}{9}$y4;
(3)原式=$\frac{2(x-2)}{{x}^{2}+3}$•$\frac{(x+3)^{2}}{x-2}$=$\frac{2{x}^{2}+12x+18}{{x}^{2}+3}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.如果不等式组$\left\{\begin{array}{l}{x+2a≥4}\\{\frac{2x-b}{3}<1}\end{array}\right.$的解集是0≤x<1,那么a+b的值为1.
9.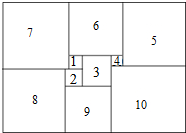 如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
 如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )| A. | x+2y | B. | 4y-x | C. | 7y-4y | D. | 10y-7x |
6.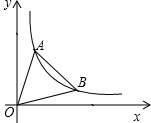 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )| A. | 2$\frac{10}{11}$ | B. | 2$\frac{11}{12}$ | C. | 2$\frac{12}{13}$ | D. | 2$\frac{13}{14}$ |