题目内容
2.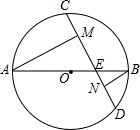 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 作OH⊥CD于H,根据垂径定理得CH=DH,由于AM⊥CD,则OH∥AM,根据平行线分线段成比例定理得HM=HN,则DN=DH-NH=$\frac{5}{2}$-$\frac{7}{6}$=$\frac{4}{3}$.
解答  证明:作OH⊥CD于H,
证明:作OH⊥CD于H,
则CH=DH=$\frac{1}{2}$CD=$\frac{5}{2}$,
∵BF⊥CD,
∴OH∥AM,
而OA=OB,
∴HM=HN=$\frac{1}{2}$MN=$\frac{7}{6}$,
∴DN=DH-NH=$\frac{5}{2}$-$\frac{7}{6}$=$\frac{4}{3}$,
故选B.
点评 本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧,也考查了平行线分线段成比例定理,作出辅助线应用垂径定理是解题的关键.

练习册系列答案
相关题目
7.将抛物线y=x2平移得到抛物线y=x2-4,下列平移正确的是( )
| A. | 向上平移4个单位 | B. | 向下平移4个单位 | C. | 向左平移4个单位 | D. | 向右平移4个单位 |
11.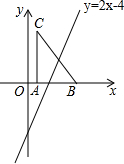 如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )
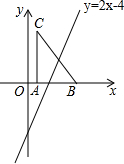 如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段BC扫过的面积为( )| A. | 8$\sqrt{2}$ | B. | 16 | C. | 16$\sqrt{2}$ | D. | 32 |
 如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度.
如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度.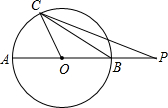 如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.
如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.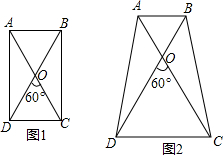 已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.
已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.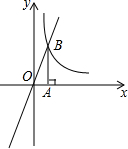 如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$. 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,与x轴,y轴分别相交于C,D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,与x轴,y轴分别相交于C,D两点.