题目内容
4.下列四组数:①5,12,13;②7,24,25;③3a,4a,5a(a>0);④32,42,52.⑤$\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$,其中可以构成直角三角形的边长有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解答 解:①52+122=132,能构成直角三角形;
②72+242=252,能构成直角三角形,能构成直角三角形;
③(3a)2+(4a)2=(5a)2,能构成直角三角形;
④(32)2+(42)2≠(52)2,不能构成直角三角形;
⑤($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,不能构成直角三角形.
故可以构成直角三角形的边长有3组.
故选C.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度.
如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度.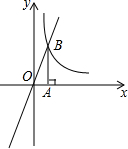 如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.