题目内容
13. 如图,在?ABCD中,AC与BD交于点O,点E是BC边的中点,OE=1,则AB的长是2.
如图,在?ABCD中,AC与BD交于点O,点E是BC边的中点,OE=1,则AB的长是2.
分析 由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OC=OA,又由点E是BC边的中点,根据三角形中位线的性质,即可求得AB的长.
解答 解:∵四边形ABCD是平行四边形,
∴OC=OA,
∵点E是BC边的中点,
即BE=CE,
∴OE=$\frac{1}{2}$AB,
∵OE=1,
∴AB=2.
故答案为:2.
点评 此题考查了平行四边形的性质与三角形中位线的性质.注意平行四边形的对角线互相平分,三角形的中位线平行于三角形的第三边且等于第三边的一半.

练习册系列答案
相关题目
3.有甲、乙、丙三个村庄分别位于等边△ABC的顶点,在城中村改造时,为保护环境,改善居民的生活条件,政府决定铺设能够连结这三个村庄的天然气管道.设计人员给出了如图四个设计方案(点D为BC边的中点,点O为△ABC的中心,实线表示天然气管道),其中天然气管道总长最短的是( )
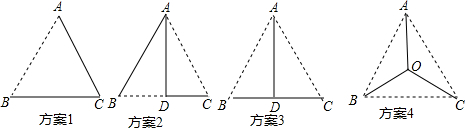

| A. | 方案1 | B. | 方案2 | C. | 方案3 | D. | 方案4 |
4.因式分解4+a2-4a正确的是( )
| A. | 4(1-a)+a2 | B. | (2-a)2 | C. | (2+a)(2-a) | D. | (2+a)2 |
1.下列说法:(1)矩形的对角线互相垂直且平分;(2)菱形的四边相等;(3)一组对边平行,另一组对边相等的四边形是平行四边形;(4)正方形的对角线相等,并且互相垂直平分.
其中正确的个数是( )
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2. 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )| A. | 18° | B. | 20° | C. | 28° | D. | 30° |
3.下列函数中,自变量的取值范围选取错误的是( )
| A. | y=x+2中,x取任意实数 | B. | y=$\sqrt{x+1}$中,x取x≤-1的实数 | ||
| C. | y=$\frac{1}{x+2}$中,x取x≠-2的实数 | D. | y=$\sqrt{{x}^{2}+1}$中,x取任意实数 |







