题目内容
3. 如图,正方形ABCD中,AB=12,点M在边CD上,且CD=3DM,△ADM沿AM对折至△AMN,延长MN与边BC交于点P,连接AP,CN,则△CNP的面积为14.4.
如图,正方形ABCD中,AB=12,点M在边CD上,且CD=3DM,△ADM沿AM对折至△AMN,延长MN与边BC交于点P,连接AP,CN,则△CNP的面积为14.4.
分析 首先利用翻折变换对应边关系得出AB=AN,∠B=∠ANP=90°,利用HL定理得出△ABP≌△ANP即可;利用勾股定理得出PM2=CP2+CM2,进而求出BP即可;过C作CE⊥PN于E,由勾股定理以及由面积法得,CE=4.8,进而得出答案.
解答 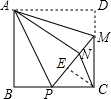 解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AM对折至△AMN,
∴AD=AN,DM=MN,∠D=∠ANM=90°,
∴AB=AN,∠B=∠ANP=90°,
又∵AP=AP,
在Rt△ABP和Rt△ANP中,
∵$\left\{\begin{array}{l}{AP=AP}\\{AB=AN}\end{array}\right.$,
∴△ABP≌△ANP,
∴BP=PN,
∵CD=3DM,
∴DM=4,CM=8,
设BP=x,则CP=12-x,PM=x+4,
∵PM2=CP2+CM2
∴(x+4)2=(12-x)2+82,
解得x=6,
∴BP=6;
过C作CE⊥PN于E,
∵BP=PN=6,
∴CP=6,MC=12-4=8,
∴PM=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵S△CPM=$\frac{1}{2}$CE•PM=$\frac{1}{2}$PC•MC,
∴CM×10=6×8,
∴CM=4.8,
∴S△CNP=$\frac{1}{2}$PN•CM=$\frac{1}{2}×6×4.8$=14.4.
故答案为:14.4.
点评 此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
16.若方程2x-1=3,则代数式4x+7的值是( )
| A. | 23 | B. | 11 | C. | 15 | D. | 20 |
15.如果a为有理数,那么下列各式一定为正数的是( )
| A. | |a| | B. | 2014a2 | C. | a2014 | D. | a2014+1 |
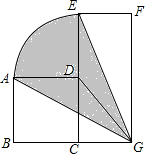 已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).
已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).