题目内容
13.两条直线l1:y=2x+4,l2:y=2x+2,l1与x、y轴交于A、B两点,l2与x、y轴交于C、D 两点,则△AOB与△COD相似吗?为什么?分析 根据一次函数图象上点的坐标特征和坐标轴上点的坐标特征求出点A、B、C、D的坐标,则可得到OA=2,OB=4,OC=1,OD=2,于是得到$\frac{OA}{OC}$=$\frac{OB}{OD}$,然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△AOB与△COD相似.
解答 解:当y=0时,2x+4=0,解得x=-2,则A(-2,0),当x=0时,y=2x+4=4,则B(0,4),即OA=2,OB=4;
当y=0时,2x+2=0,解得x=-1,则C(-1,0),当x=0时,y=2x+2=4,则D(0,2),即OC=1,OD=2,
∵$\frac{OA}{OC}$=$\frac{2}{1}$=2,$\frac{OB}{OD}$=$\frac{4}{2}$=2,
∴$\frac{OA}{OC}$=$\frac{OB}{OD}$,
∵∠AOB=∠COD,
∴△AOB∽△COD.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形ABCD中,AB=12,点M在边CD上,且CD=3DM,△ADM沿AM对折至△AMN,延长MN与边BC交于点P,连接AP,CN,则△CNP的面积为14.4.
如图,正方形ABCD中,AB=12,点M在边CD上,且CD=3DM,△ADM沿AM对折至△AMN,延长MN与边BC交于点P,连接AP,CN,则△CNP的面积为14.4.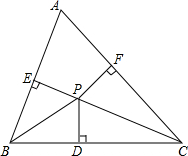 已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF.
已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF. 如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.