题目内容
2013年6月25日,包茂高速公路粤境段正式开工建设,甲乙两个工程队共同承担泗水段的一项筑路任务,甲队单独完成此项任务比乙队单独完成此项任务多用10天,若甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)请问:乙队单独完成此项任务需要多少天?
(2)若甲乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
(1)请问:乙队单独完成此项任务需要多少天?
(2)若甲乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,根据甲队单独施工45天和乙队单独施工30天的工作量相同建立方程求出其解即可;
(2)设甲队再单独施工a天,根据甲队总的工作量不少于乙队的工作量的2倍建立不等式求出其解即可.
(2)设甲队再单独施工a天,根据甲队总的工作量不少于乙队的工作量的2倍建立不等式求出其解即可.
解答:解:(1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,
由题意,得
=
,
解得:x=20.
经检验,x=20是原方程的解,
即x+10=30(天).
答:甲队单独完成此项任务需要30天,乙队单独完成此项任务需要20天;
(2)设甲队再单独施工a天,由题意,得
+
≥2×
,
解得:a≥3.
答:甲队至少再单独施工3天.
由题意,得
| 45 |
| x+10 |
| 30 |
| x |
解得:x=20.
经检验,x=20是原方程的解,
即x+10=30(天).
答:甲队单独完成此项任务需要30天,乙队单独完成此项任务需要20天;
(2)设甲队再单独施工a天,由题意,得
| 3 |
| 30 |
| 2a |
| 30 |
| 3 |
| 20 |
解得:a≥3.
答:甲队至少再单独施工3天.
点评:本题主要考查了分式的应用的知识,解答本题的关键是掌握工作时间×工作效率=工作总量,利用此关系等式列出分式方程,解答时验根是学生容易忽略的地方,此题难度适中.

练习册系列答案
相关题目
 如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是
如图,已知△ABC中,若BC=6,△ABC的面积为12,四边形DEFG是△ABC的内接的正方形,则正方形DEFG的边长是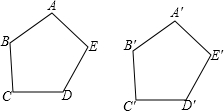 如图,在五边形ABCDE和五边形A1B1C1D1E1中,如果AB=A1B1,BC=B1C1,CD=C1D1,DE=D1E1,EA=E1A1.请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)
如图,在五边形ABCDE和五边形A1B1C1D1E1中,如果AB=A1B1,BC=B1C1,CD=C1D1,DE=D1E1,EA=E1A1.请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)