题目内容
15.解不等式:(1)$\frac{1}{2}x-1≤$$\frac{2}{3}$x-$\frac{1}{2}$;
(2)3y-$\frac{3-4y}{7}$<$\frac{5}{2}$y-1.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
解答 解:(1)$\frac{1}{2}x-1≤$$\frac{2}{3}$x-$\frac{1}{2}$,
3x-6≤4x-3,
3x-4x≤-3+6,
-x≤3,
x≥-3;
(2)3y-$\frac{3-4y}{7}$<$\frac{5}{2}$y-1,
42y-2(3-4y)<35y-14,
42y-6+8y<35y-14,
42y+8y-35y<-14+6,
15y<-8,
y<-$\frac{8}{15}$.
点评 本题考查了解一元一次不等式的应用,能根据不等式的基本性质正确解不等式是解此题的关键,注意:解一元一次不等式的步骤是:去分母,去括号,移项,合并同类项,系数化成1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列函数的图象中,不经过第一象限的是( )
| A. | y=x+3 | B. | y=x-3 | C. | y=-x+1 | D. | y=-x-1 |
3.解方程组:$\left\{\begin{array}{l}{x+\sqrt{3}y=5\sqrt{3}}\\{3x-\sqrt{3}y=3\sqrt{3}}\end{array}\right.$.
4.-|$\frac{1}{2015}$|的倒数是( )
| A. | 2015 | B. | -2015 | C. | -$\frac{1}{2015}$ | D. | $\frac{1}{2015}$ |
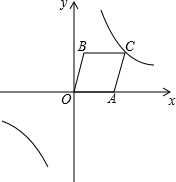 如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.