题目内容
6.已知实数x,y满足x2+5x+y-5=0,则y的最大值是$\frac{45}{4}$,x+y的最大值是9.分析 因为x,y满足x2+5x+y-5=0,所以y=-x2-5x+5,所以y的最大值转化为函数y=-x2-5x+5的最大值问题,故x+y也可转化为函数的最值问题.
解答 解:∵x2+5x+y-5=0
∴y=-x2-5x+5
∴y的最大值为:$\frac{4ac-{b}^{2}}{4a}=\frac{4×(-1)×5-(-5)^{2}}{4×(-1)}=\frac{45}{4}$
又∵x+y=-x2-5x+5+x
即x+y=-x2-4x+5
∴x+y的最大值是:$\frac{4ac-{b}^{2}}{4a}=\frac{4×(-1)×5-(-4)^{2}}{4×(-1)}=9$
故答案为:$\frac{45}{4}$,9.
点评 本题考查二次函数的最值问题,关键是将问题转化为二次函数.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
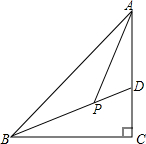 如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.
如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由. 在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少?
在△ABC中,∠ABC=100°,且∠AEF=∠AFE,∠CFD=∠CDF,那么∠EFD的度数是多少? 如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.
如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.