题目内容
3.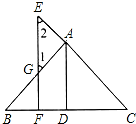 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC,填写分析和证明中的空白.
证明:∵AD⊥BC,EF⊥BC(已知)
∴AD∥EF (垂直于同一直线的两直线平行 ).
∴∠BAD=∠1(两直线平行,内错角相等),
∠CAD=∠2 (两直线平行,同位角相等),
∵∠1=∠2 (已知),
∴∠BAD=∠CAD,即AD平分∠BAC(角平分线定义 ).
分析 根据平行线的判定推出AD∥EF,根据平行线的性质得出∠BAD=∠1,∠CAD=∠2,推出∠BAD=∠CAD即可.
解答 证明:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF(垂直于同一直线的两直线平行),
∴∠BAD=∠1(两直线平行,内错角相等),
∠CAD=∠2(两直线平行,同位角相等),
∵∠1=∠2,
∴∠BAD=∠CAD,
即AD平分∠BAC(角平分线定义),
故答案为:AD,EF,垂直于同一条直线的两条直线平行,∠BAD,∠1,∠CAD,∠2,∠1=∠2,∠BAD=∠CAD,角平分线定义.
点评 本题考查了角平分线定义,平行线的性质和判定的应用,能灵活运用平行线的性质和判定定理进行推理是解此题的关键.

练习册系列答案
相关题目
11.如果不等式组$\left\{\begin{array}{l}{2x-5>3(x-1)}\\{-x<m}\end{array}\right.$的解集是无解,那么m的取值范围是( )
| A. | m=2 | B. | m≥2 | C. | m<2 | D. | m≤2 |
15.若3x-2y-7=0,则4y-6x+12的值为( )
| A. | 12 | B. | 19 | C. | -2 | D. | 无法确定 |
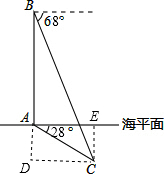 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出:
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出: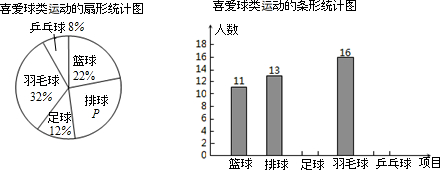
 如图,DB平分∠ADE,DE∥AB,∠CDE=86°,则∠ABD=47°,∠A=86°.
如图,DB平分∠ADE,DE∥AB,∠CDE=86°,则∠ABD=47°,∠A=86°.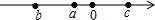 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.